арифметика
Найдено: 5 записей
Программирование →
Ошибки вычислений в окрестностях машинного нуля
Периодически на хабре возникают замечательные статьи о тонкостях арифметики с плавающей точкой. Собственно, упомянутая публикация стала одним из первых источников, прочитанных при попытках разобраться с проблемой. Яснее от этого сразу не стало, но тем не менее, организация нейронных связей как-то упорядочилась. Ближе к делу.
Проблема образовалась при выполнении расчётов в рамках одного проекта и будущей магистерской диссертации по гидродинамике пористой среды. Не скрою, что корни скрыты отчасти в личной криворукости автора и пренебрежении банальными общеизвестными советами касательно обработки малых чисел, но тем не менее, это привело к достаточно интересным наблюдениям и размышлениям.
Если отбросить физическую суть, то задача состоит в необходимости решения системы семи уравнений в частных производных. Сказано-сделано, сложности в этом особой нет — пишем явную конечно-разностную схему, распараллеливаем на OpenMP и после окончательной синтаксической отладки и оптимизации скорости «машинка начинает шуршать».
Вычислительная конфигурация: видавший виды HP 550 с Core 2 Duo 1.8 ГГц на борту, под управлением Ubuntu 11.04.
Компиляторы: gfortran 4.5.2 и Intel Fortran Compiler 12.1.0.
В начальных условиях предполагается, что внутри расчётной области совсем нет воды в жидком состоянии — она появляется в процессе фазовых превращений. И именно это отсутствие сыграло главную роль в нашем спектакле.
Итак, воды в области нет. Что же хочется написать в начальном условии? Естественно, сразу же было написано 0.0D+00 (программа написана с двойной точностью вещественных чисел). Счёт на первоначальных этапах идёт в непосредственной окрестности машинного нуля. Каковы результаты? Посмотрим на график:
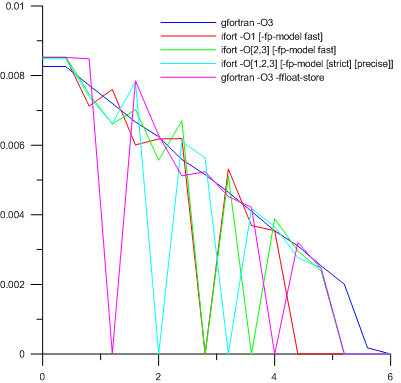
Здесь изображено распределение насыщенности пор водой вдоль координаты в наиболее интересной части расчётной области по прошествии чуть более суток физического времени модели.
Нужное отступление о подписях в легенде графика: всего было опробовано 18 различных комбинаций ключей (6 для gfortran и 12 для ifort), однако многие из них давали абсолютно одинаковые результаты, и потому объединены. Квадратные скобки в легенде означают, что могла быть написана любая из заключённых в них опций. Например, «шифровка» -O[1,2,3] [-fp-model [strict] [precise]] говорит о том, что компилятор использовался с оптимизацией всех возможных уровней, и дополнительно могла быть включена одна моделей вычислений с плавающей точкой (а могла быть и не включена). Три варианта (два от -fp-model и один без неё) умножить на три уровня оптимизации — итого девять комбинаций. Все они оказались эквивалентны.
А теперь результат. Нечто реалистичное и физически возможное удалось получить только на gfortran без включения соответствия стандарту IEEE 754 (ключ -ffloat-store). Весь остальной хаос линий не содержит ни капельки физического смысла, потому что даже математически уравнения этого не допускают. Изначально подозревавшаяся неустойчивость разностной схемы была оправдана, поскольку никакие методы борьбы с ней к успеху не привели.
Было замечено, что при наличии воды в начальный момент счёт остаётся устойчивым и различия между опциями и компиляторами скрываются в окрестности шестой значащей цифры. И т.к. характерные порядки величины, судя по полученным графикам, должны быть в районе 1.0e-2, то в начальное условие было вписано некоторое ненулевое значение, но очень маленькое. Подбором удалось установить, что для 8-байтового real оно должно быть не менее 1.0e-21. И тогда:
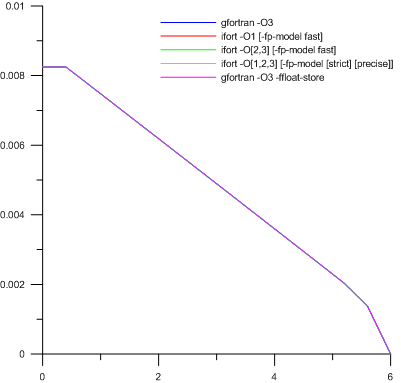
Да, здесь, как и написано в легенде, на самом деле пять графиков. Просто мы получаем то самое различие в пределах шестой значащей цифры.
Причины? Вполне очевидны. Они лежат в тонкостях одновременной обработки больших и малых чисел. И тот факт, что явление настолько существенно по своим масштабам, был, в общем-то, ожидаемым. Но, прежде всего, интерес вызывает нестабильность работы действительно отличного инструмента от Intel на фоне относительного успеха gfortran 4.5.2. Стоит отметить, что подобные проблемы были также найдены при расчётах на старой версии gfortran 4.1.2 с включённой оптимизацией и без других опций, установленной на доступном кластере (под управлением Slamd64), однако им тогда не было уделено должного внимания.
Соответствие IEEE 754, как ни странно, сыграло критическую роль для gfortran. Без него счёт достаточно стабильный и точный. Для детища Intel это оказалось не столь существенно, ибо оно и так не работало корректно.
Итак, выводы и мысли о причинах увиденного.
Тестирование компиляторов на соответствие IEEE 754 проводилось с помощью FORTRAN-версии «Floating point paranoia» Уильяма Кэхэна.
Проблема образовалась при выполнении расчётов в рамках одного проекта и будущей магистерской диссертации по гидродинамике пористой среды. Не скрою, что корни скрыты отчасти в личной криворукости автора и пренебрежении банальными общеизвестными советами касательно обработки малых чисел, но тем не менее, это привело к достаточно интересным наблюдениям и размышлениям.
Если отбросить физическую суть, то задача состоит в необходимости решения системы семи уравнений в частных производных. Сказано-сделано, сложности в этом особой нет — пишем явную конечно-разностную схему, распараллеливаем на OpenMP и после окончательной синтаксической отладки и оптимизации скорости «машинка начинает шуршать».
Вычислительная конфигурация: видавший виды HP 550 с Core 2 Duo 1.8 ГГц на борту, под управлением Ubuntu 11.04.
Компиляторы: gfortran 4.5.2 и Intel Fortran Compiler 12.1.0.
В начальных условиях предполагается, что внутри расчётной области совсем нет воды в жидком состоянии — она появляется в процессе фазовых превращений. И именно это отсутствие сыграло главную роль в нашем спектакле.
Итак, воды в области нет. Что же хочется написать в начальном условии? Естественно, сразу же было написано 0.0D+00 (программа написана с двойной точностью вещественных чисел). Счёт на первоначальных этапах идёт в непосредственной окрестности машинного нуля. Каковы результаты? Посмотрим на график:

Здесь изображено распределение насыщенности пор водой вдоль координаты в наиболее интересной части расчётной области по прошествии чуть более суток физического времени модели.
Нужное отступление о подписях в легенде графика: всего было опробовано 18 различных комбинаций ключей (6 для gfortran и 12 для ifort), однако многие из них давали абсолютно одинаковые результаты, и потому объединены. Квадратные скобки в легенде означают, что могла быть написана любая из заключённых в них опций. Например, «шифровка» -O[1,2,3] [-fp-model [strict] [precise]] говорит о том, что компилятор использовался с оптимизацией всех возможных уровней, и дополнительно могла быть включена одна моделей вычислений с плавающей точкой (а могла быть и не включена). Три варианта (два от -fp-model и один без неё) умножить на три уровня оптимизации — итого девять комбинаций. Все они оказались эквивалентны.
А теперь результат. Нечто реалистичное и физически возможное удалось получить только на gfortran без включения соответствия стандарту IEEE 754 (ключ -ffloat-store). Весь остальной хаос линий не содержит ни капельки физического смысла, потому что даже математически уравнения этого не допускают. Изначально подозревавшаяся неустойчивость разностной схемы была оправдана, поскольку никакие методы борьбы с ней к успеху не привели.
Было замечено, что при наличии воды в начальный момент счёт остаётся устойчивым и различия между опциями и компиляторами скрываются в окрестности шестой значащей цифры. И т.к. характерные порядки величины, судя по полученным графикам, должны быть в районе 1.0e-2, то в начальное условие было вписано некоторое ненулевое значение, но очень маленькое. Подбором удалось установить, что для 8-байтового real оно должно быть не менее 1.0e-21. И тогда:

Да, здесь, как и написано в легенде, на самом деле пять графиков. Просто мы получаем то самое различие в пределах шестой значащей цифры.
Причины? Вполне очевидны. Они лежат в тонкостях одновременной обработки больших и малых чисел. И тот факт, что явление настолько существенно по своим масштабам, был, в общем-то, ожидаемым. Но, прежде всего, интерес вызывает нестабильность работы действительно отличного инструмента от Intel на фоне относительного успеха gfortran 4.5.2. Стоит отметить, что подобные проблемы были также найдены при расчётах на старой версии gfortran 4.1.2 с включённой оптимизацией и без других опций, установленной на доступном кластере (под управлением Slamd64), однако им тогда не было уделено должного внимания.
Соответствие IEEE 754, как ни странно, сыграло критическую роль для gfortran. Без него счёт достаточно стабильный и точный. Для детища Intel это оказалось не столь существенно, ибо оно и так не работало корректно.
Итак, выводы и мысли о причинах увиденного.
- Наиболее вероятным кандидатом на роль причины наблюдаемого поведения расчётов представляются тонкости округления чисел. Т.к. в начальном распределении величины задано нулевое значение, то на первых шагах счёт производится практически на границе машинной точности. Соответственно, это приводит к накоплению заметных погрешностей, которые и проявляются в конечном результате.
- Потери точности в алгоритме вызываются, очевидно, и тем фактом, что решается размерная система семи дифференциальных уравнений в частных производных, переменные в каждом из которых имеют собственные характерные значения, существенно отличающиеся от остальных. При правильном выборе масштабных множителей, в безразмерной системе уравнений получить близкие хотя бы по порядку величины значения всех переменных, хотя при первоначальных попытках провести обезразмеривание в системе возникали малые коэффициенты перед производными, что и стало поводом для отказа от данной процедуры.
- Вопрос же о том, почему gfortran, не соответствующий стандарту вычислений с плавающей точкой, способен выдавать приемлемый результат, остаётся открытым. Разумно предполагать наличие каких-то собственных, отличных от стандарта, правил округления, которые и обеспечивают сохранение стабильного счёта, а также их корректировку и уточнение в процессе развития компилятора. «Хрупкий баланс ошибок» либо продуманное исправление подхода? Увы, на моём уровне знаний об инструментарии, нацеленном в первую очередь именно на применение компиляторов, а не их тестирование и изучение свойств, это неизвестно. Но заставляет задуматься и вспомнить предостережения о возможных потерях точности в тех или иных местах программ, данные ещё на первых этапах обучения численным методам в вузе.
Тестирование компиляторов на соответствие IEEE 754 проводилось с помощью FORTRAN-версии «Floating point paranoia» Уильяма Кэхэна.
25.01.2012 21:03+0400
Ни о чём →
Как помочь ребенку выучить таблицу умножения

Недавно мне задали этот вопрос, и после моего рассказа как я научил таблице умножения одного моего знакомого мальчика, оказалось, что по этим советам еще один ученик довольно быстро выучил таблицу умножения без монотонного заучивания. Поэтому я подумал, что будет полезным рассказать и вам эти простые приемы, вдруг перед вами тоже встанет такая задача, например, при обучении своего ребенка.
После довольно понятных сложения и вычитания, зубрежка таблицы умножения часто выглядит как некий скучный ритуал, лишенный какой-либо наглядности. Поэтому многие школьники довольно быстро утрачивают интерес и плохо ее знают, а это отражается на всем образовании. Я уверен, что обучение умножению это очень важный опыт, который сказывается на общей уверенности человека в собственных знаниях и возможностях ума, и, может быть, даже рациональном выборе профессии.
Описанные приемы довольно просты, и, строго говоря, давно известны. Запоминание в моем рассказе происходит тоже через частые повторения примеров, но все они – лишь разные события одной игры в которой этим перемножения оживают. Я обобщил известные мне приемы и составил для своего ученика такое расписание, чтобы чуть более сложное чередовалось с простым. Ввиду занятности такого обучения, одновременно с запоминанием таблицы ребенок узнает и другие интересные вещи из мира арифметики и вообще математики: о простых числах, признаке деления на 3, степенях двойки и так далее.
Также косвенно в рассказе упоминаются и некоторые способы мотивации. Само наше обучение, как станет ясно из повествования, представляло собой игру. Уверен, в комментариях вы сможете дополнить мою историю своими интересными идеями и методами, о которых я не знал, что поможет сделать рассказ более полным для того, кто натолкнется на него в поисках ответа на вопрос заголовка статьи.
10.08.2011 18:41+0400
Научно популярное →
Математический язык для операций с бесконечностью
47-летний профессор Нижегородского государственного университета имени Н.И.Лобачевского, доктор физико-математических наук Ярослав Сергеев получил международную премию Пифагора, которая считается одной из самых престижных наград в области математики.
Премия Пифагора присуждена за работы, связанные с параллельными и последовательными методами решения задач глобальной оптимизации, а также за разработку новой арифметики, которая позволяет выполнять вычисления с бесконечно большими и бесконечно малыми величинами.
В основе конструкции Сергеева лежит гросс-единица (grossone). Гросс-единица — это бесконечное число, равное по определению количеству элементов в множестве N натуральных чисел. Обозначается символом . Таким образом, множество натуральных чисел можно расширить так.
. Таким образом, множество натуральных чисел можно расширить так.

Премия Пифагора присуждена за работы, связанные с параллельными и последовательными методами решения задач глобальной оптимизации, а также за разработку новой арифметики, которая позволяет выполнять вычисления с бесконечно большими и бесконечно малыми величинами.
В основе конструкции Сергеева лежит гросс-единица (grossone). Гросс-единица — это бесконечное число, равное по определению количеству элементов в множестве N натуральных чисел. Обозначается символом
 . Таким образом, множество натуральных чисел можно расширить так.
. Таким образом, множество натуральных чисел можно расширить так.
09.11.2010 10:27+0300
humour →
Вычисления в Windows 7
07.11.2008 00:41+0300
Ни о чём →
Как сделать из 123456789 число 100 или 0
В «Занимательной арифметике» известного популяризатора наук Якова Исидоровича Перельмана в конце первой главы я нашел пример следующих «Арифметических курьезов»:
100 = 1+2+3+4+5+6+7+8*9
100 = 12+3-4+5+67+8+9
100 = 12-3-4+5-6+7+89
100 = 123+4-5+67-89
100 = 123-45-67+89
Первое из этих решений я нашел еще в начальной школе на олимпиаде по математике, и теперь подумав, что, может быть, та победа повлияла на мое будущее становление, я решил воздать должное этой задаче и найти все возможные решения, написав соответствующий скрипт на Python.
100 = 1+2+3+4+5+6+7+8*9
100 = 12+3-4+5+67+8+9
100 = 12-3-4+5-6+7+89
100 = 123+4-5+67-89
100 = 123-45-67+89
Первое из этих решений я нашел еще в начальной школе на олимпиаде по математике, и теперь подумав, что, может быть, та победа повлияла на мое будущее становление, я решил воздать должное этой задаче и найти все возможные решения, написав соответствующий скрипт на Python.
30.11.1999 00:00+0300

