Ни о чём →
Как сделать из 123456789 число 100 или 0
В «Занимательной арифметике» известного популяризатора наук Якова Исидоровича Перельмана в конце первой главы я нашел пример следующих «Арифметических курьезов»:
100 = 1+2+3+4+5+6+7+8*9
100 = 12+3-4+5+67+8+9
100 = 12-3-4+5-6+7+89
100 = 123+4-5+67-89
100 = 123-45-67+89
Первое из этих решений я нашел еще в начальной школе на олимпиаде по математике, и теперь подумав, что, может быть, та победа повлияла на мое будущее становление, я решил воздать должное этой задаче и найти все возможные решения, написав соответствующий скрипт на Python.
Пусть задача поставлена так: есть строка цифр 123456789 (пусть я и правда не очень интересуюсь нулем), между которыми можно в любых местах поставить 4 арифметических операции (+, -, *, /) или не ставить ничего (то есть ставить пустую строку, тогда образуются двух- и более -значные числа) так, чтобы общее выражение давало в результате 100, как в примерах из книги выше. Ничего другого нельзя, никаких скобок, никаких перестановок, никаких дублей, никаких выкидываний.
Я не учился программированию, и реализовал задачу, как придумал. Поэтому у меня есть вопрос: «Как это можно было сделать лучше?».
А придумал я так: для того чтобы перебрать все возможные варианты вставки символов промежутков (а их пять: либо пустая строка, либо +, -, *, /), я представлял их как варианты числа по основанию 5, дополненные слева нулями. Длина такого числа восемь символов, поскольку цифр девять, и между ними тогда имеется восемь промежутков. Нули соответствуют пустым строкам, все остальные — арифметическим операциям. Вот что получилось:
Для 100 нашлось 101 такое решение, причем некоторые из них довольно забавные, особенно с дробями:
123+45-67+8-9 = 100
123+4-5+67-89 = 100
123+4*5-6*7+8-9 = 100
123-45-67+89 = 100
123-4-5-6-7+8-9 = 100
12+34+5*6+7+8+9 = 100
12+34-5+6*7+8+9 = 100
12+34-5-6+7*8+9 = 100
12+34-5-6-7+8*9 = 100
12+3+4+5-6-7+89 = 100
12+3+4-56/7+89 = 100
12+3-4+5+67+8+9 = 100
12+3*45+6*7-89 = 100
12+3*4+5+6+7*8+9 = 100
12+3*4+5+6-7+8*9 = 100
12+3*4-5-6+78+9 = 100
12-3+4*5+6+7*8+9 = 100
12-3+4*5+6-7+8*9 = 100
12-3-4+5-6+7+89 = 100
12-3-4+5*6+7*8+9 = 100
12-3-4+5*6-7+8*9 = 100
12*3-4+5-6+78-9 = 100
12*3-4-5-6+7+8*9 = 100
12*3-4*5+67+8+9 = 100
12/3+4*5-6-7+89 = 100
12/3+4*5*6-7-8-9 = 100
12/3+4*5*6*7/8-9 = 100
12/3/4+5*6+78-9 = 100
1+234-56-7-8*9 = 100
1+234*5*6/78+9 = 100
1+234*5/6-7-89 = 100
1+23-4+56+7+8+9 = 100
1+23-4+56/7+8*9 = 100
1+23-4+5+6+78-9 = 100
1+23-4-5+6+7+8*9 = 100
1+23*4+56/7+8-9 = 100
1+23*4+5-6+7-8+9 = 100
1+23*4-5+6+7+8-9 = 100
1+2+34-5+67-8+9 = 100
1+2+34*5+6-7-8*9 = 100
1+2+3+4+5+6+7+8*9 = 100
1+2+3-45+67+8*9 = 100
1+2+3-4+5+6+78+9 = 100
1+2+3-4*5+6*7+8*9 = 100
1+2+3*4-5-6+7+89 = 100
1+2+3*4*56/7-8+9 = 100
1+2+3*4*5/6+78+9 = 100
1+2-3*4+5*6+7+8*9 = 100
1+2-3*4-5+6*7+8*9 = 100
1+2*34-56+78+9 = 100
1+2*3+4+5+67+8+9 = 100
1+2*3+4*5-6+7+8*9 = 100
1+2*3-4+56/7+89 = 100
1+2*3-4-5+6+7+89 = 100
1+2*3*4*5/6+7+8*9 = 100
1-23+4*5+6+7+89 = 100
1-23-4+5*6+7+89 = 100
1-23-4-5+6*7+89 = 100
1-2+3+45+6+7*8-9 = 100
1-2+3*4+5+67+8+9 = 100
1-2+3*4*5+6*7+8-9 = 100
1-2+3*4*5-6+7*8-9 = 100
1-2-34+56+7+8*9 = 100
1-2-3+45+6*7+8+9 = 100
1-2-3+45-6+7*8+9 = 100
1-2-3+45-6-7+8*9 = 100
1-2-3+4*56/7+8*9 = 100
1-2-3+4*5+67+8+9 = 100
1-2*3+4*5+6+7+8*9 = 100
1-2*3-4+5*6+7+8*9 = 100
1-2*3-4-5+6*7+8*9 = 100
1*234+5-67-8*9 = 100
1*23+4+56/7*8+9 = 100
1*23+4+5+67-8+9 = 100
1*23-4+5-6-7+89 = 100
1*23-4-56/7+89 = 100
1*23*4-56/7/8+9 = 100
1*2+34+56+7-8+9 = 100
1*2+34+5+6*7+8+9 = 100
1*2+34+5-6+7*8+9 = 100
1*2+34+5-6-7+8*9 = 100
1*2+34-56/7+8*9 = 100
1*2+3+45+67-8-9 = 100
1*2+3+4*5+6+78-9 = 100
1*2+3-4+5*6+78-9 = 100
1*2+3*4+5-6+78+9 = 100
1*2-3+4+56/7+89 = 100
1*2-3+4-5+6+7+89 = 100
1*2-3+4*5-6+78+9 = 100
1*2*34+56-7-8-9 = 100
1*2*3+4+5+6+7+8*9 = 100
1*2*3-45+67+8*9 = 100
1*2*3-4+5+6+78+9 = 100
1*2*3-4*5+6*7+8*9 = 100
1*2*3*4+5+6+7*8+9 = 100
1*2*3*4+5+6-7+8*9 = 100
1*2*3*4-5-6+78+9 = 100
1*2/3+4*5/6+7+89 = 100
1/2*34-5+6-7+89 = 100
1/2*3/4*56+7+8*9 = 100
1/2/3*456+7+8+9 = 100
Потом я решил просмотреть полную зависимость числа возможных решений таких разложений от всех возможных сумм, в том числе и нецелых. Для этого цикл стал функцией, работающей на заполнение словаря:
Списки зависимости ylist=f(xlist) рисуются с помощью matplotlib. Зависимость имеет пик в нуле со 167 решениями:
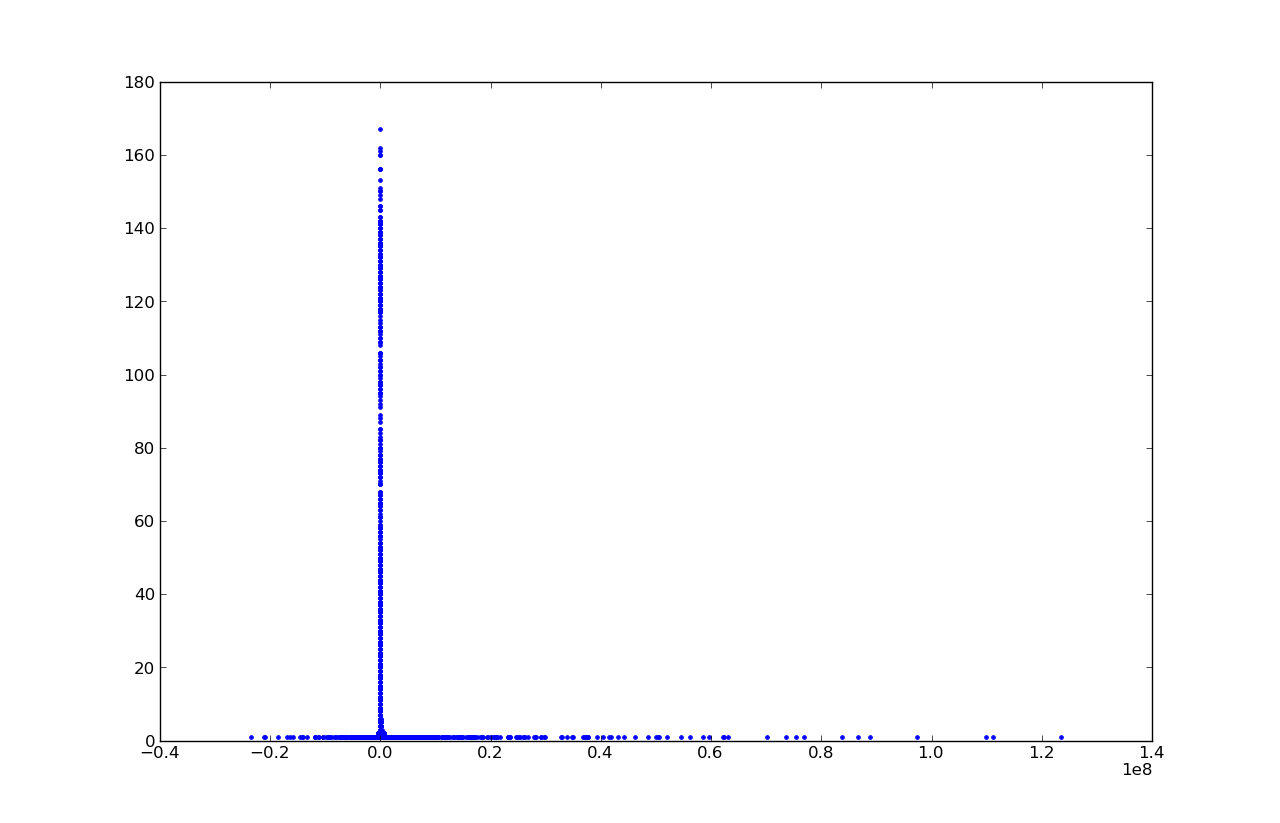
Левая ветвь не симметрична правой, потому что перед вариантом 1*2*3*4*5*6*7*8*9 по условию задачи минус мы поставить не можем. Чем ближе к нулю, тем чаще встречаются действительные числа, которые можно представить несколькими возможными способами.
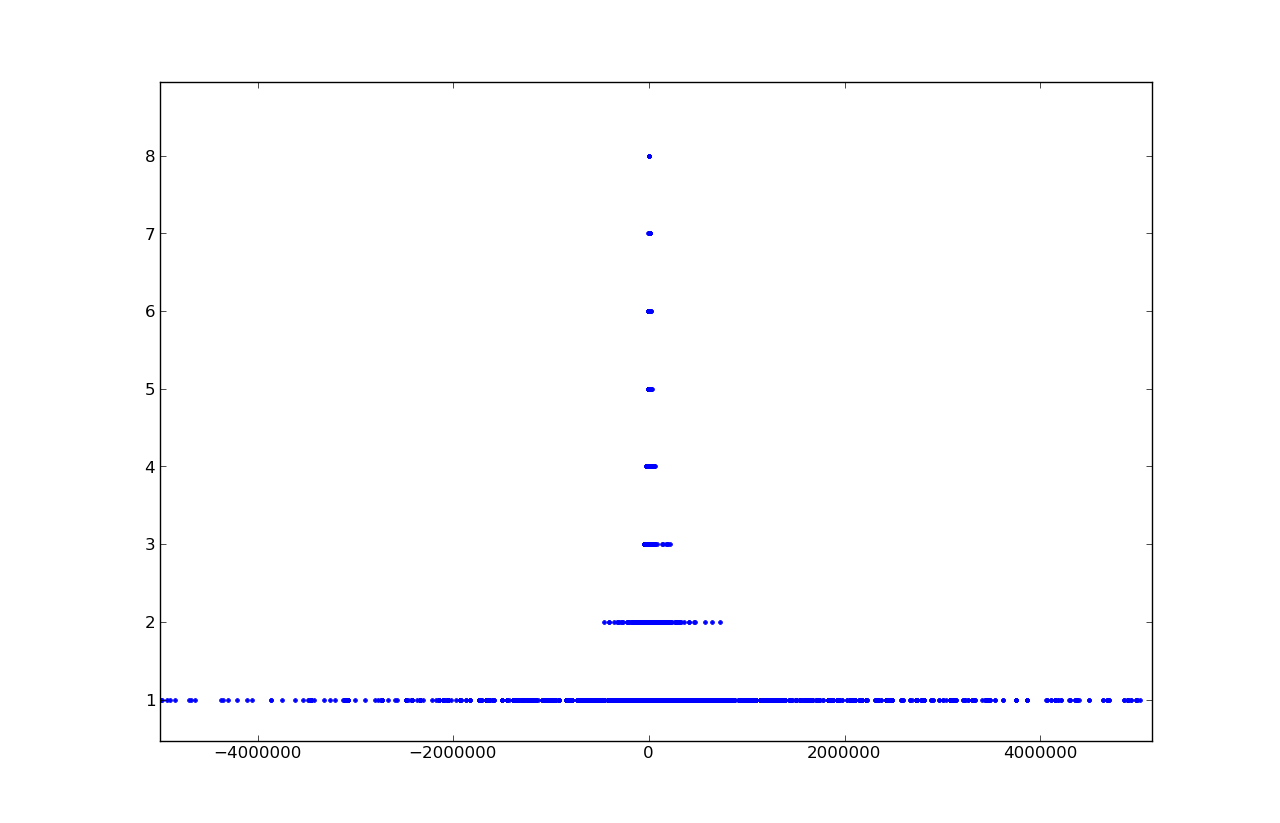
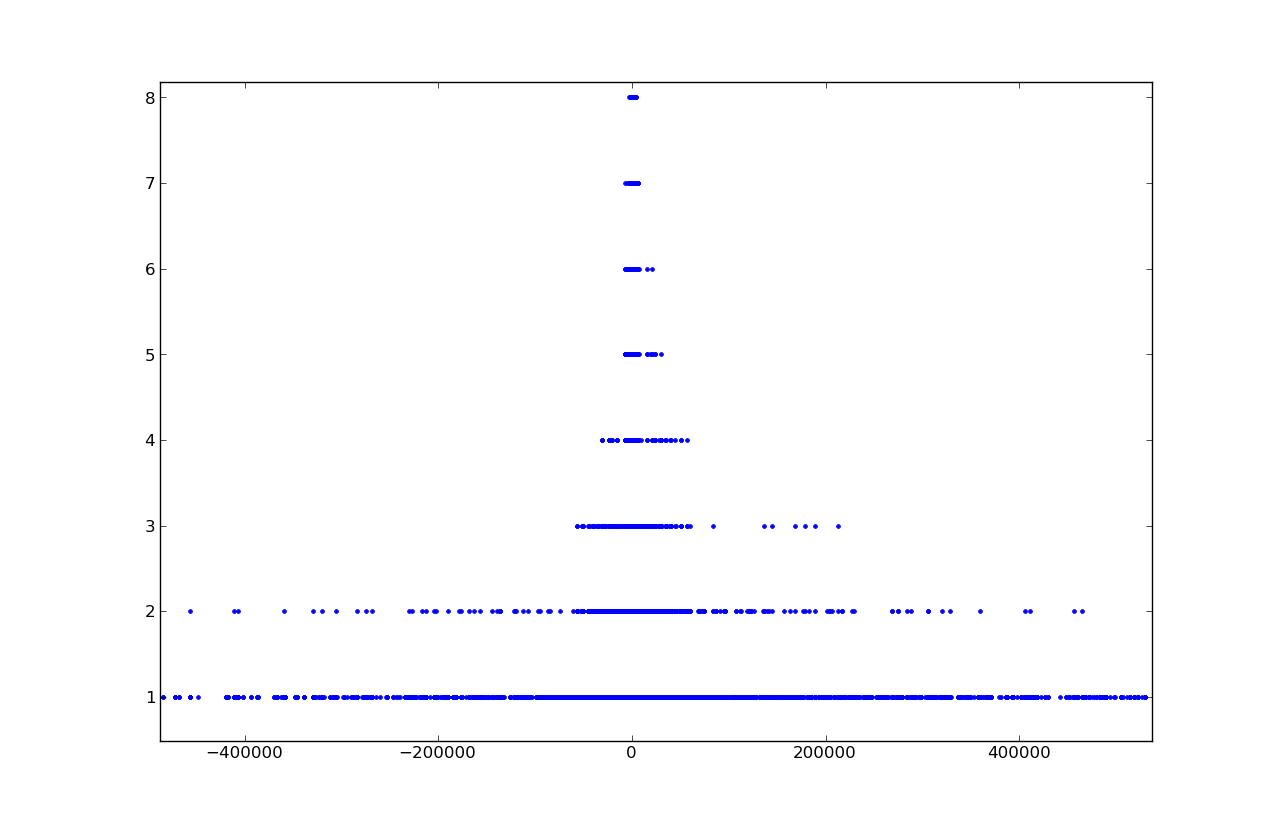
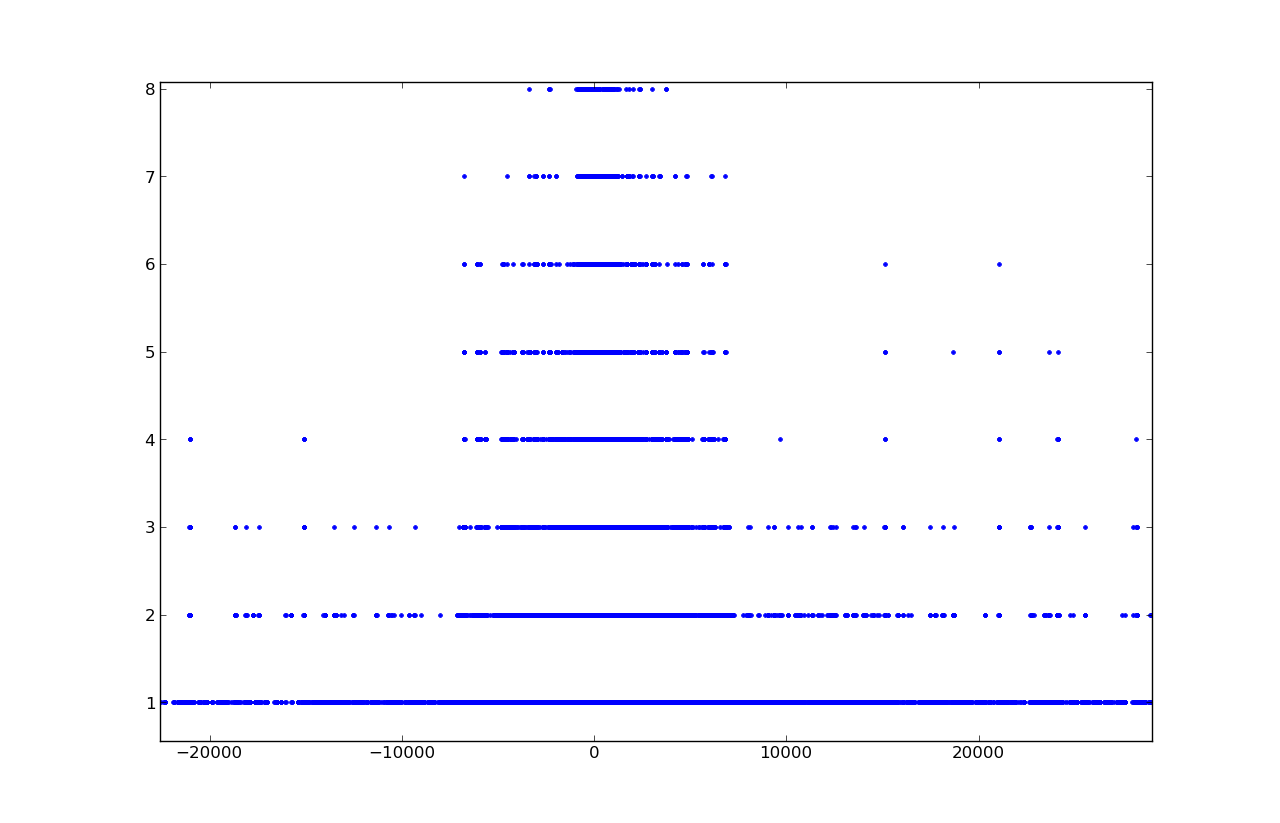

Отдельное рассмотрение для решений в области [-1.1, 1.1]: наибольшее число решений приходится, собственно, на ноль, потом на целые числа -1, 1, потом на полуцелые -0.5, 0.5.

Проверено, что любое из целых чисел от 0 до 100 может быть выражено таким способом:

Может быть, эта задача понравится и просто, чтобы задать кому-то, например собственному ребенку или приятелю, на скорость счета и умение обращаться с числами, как когда-то мне она была задана в начальной школе и нужно было найти одно решение, хотя, как я теперь вижу, их было намного больше. А можете попробовать сами в уме или на бумаге найти хотя бы одно из 167 решений для нуля.
100 = 1+2+3+4+5+6+7+8*9
100 = 12+3-4+5+67+8+9
100 = 12-3-4+5-6+7+89
100 = 123+4-5+67-89
100 = 123-45-67+89
Первое из этих решений я нашел еще в начальной школе на олимпиаде по математике, и теперь подумав, что, может быть, та победа повлияла на мое будущее становление, я решил воздать должное этой задаче и найти все возможные решения, написав соответствующий скрипт на Python.
Пусть задача поставлена так: есть строка цифр 123456789 (пусть я и правда не очень интересуюсь нулем), между которыми можно в любых местах поставить 4 арифметических операции (+, -, *, /) или не ставить ничего (то есть ставить пустую строку, тогда образуются двух- и более -значные числа) так, чтобы общее выражение давало в результате 100, как в примерах из книги выше. Ничего другого нельзя, никаких скобок, никаких перестановок, никаких дублей, никаких выкидываний.
Я не учился программированию, и реализовал задачу, как придумал. Поэтому у меня есть вопрос: «Как это можно было сделать лучше?».
А придумал я так: для того чтобы перебрать все возможные варианты вставки символов промежутков (а их пять: либо пустая строка, либо +, -, *, /), я представлял их как варианты числа по основанию 5, дополненные слева нулями. Длина такого числа восемь символов, поскольку цифр девять, и между ними тогда имеется восемь промежутков. Нули соответствуют пустым строкам, все остальные — арифметическим операциям. Вот что получилось:
Copy Source | Copy HTML
from __future__ import division # for 2.x version
s = '123456789'
d = {'0':'', '1':'+', '2':'-', '3':'*', '4':'/'}
sum_num = 100
count = 0
def to_new_base(n, new_base):
s = []
if n == 0:
s.append('0')
while n:
s.append(str(n % new_base))
n = n // new_base
num = '{0:0>8}'.format(''.join(s[::-1]))
return num
for n in xrange(int('44444444', 5)):
num = to_new_base(n, 5)
expr = ''
for i, j in zip(s, num):
expr += i + d[j]
expr += '9'
if eval(expr) == sum_num:
print('{0} = {1}'.format(expr, sum_num))
count += 1
print 'So, {0} expressions for {1}'.format(count, sum_num)
Для 100 нашлось 101 такое решение, причем некоторые из них довольно забавные, особенно с дробями:
123+45-67+8-9 = 100
123+4-5+67-89 = 100
123+4*5-6*7+8-9 = 100
123-45-67+89 = 100
123-4-5-6-7+8-9 = 100
12+34+5*6+7+8+9 = 100
12+34-5+6*7+8+9 = 100
12+34-5-6+7*8+9 = 100
12+34-5-6-7+8*9 = 100
12+3+4+5-6-7+89 = 100
12+3+4-56/7+89 = 100
12+3-4+5+67+8+9 = 100
12+3*45+6*7-89 = 100
12+3*4+5+6+7*8+9 = 100
12+3*4+5+6-7+8*9 = 100
12+3*4-5-6+78+9 = 100
12-3+4*5+6+7*8+9 = 100
12-3+4*5+6-7+8*9 = 100
12-3-4+5-6+7+89 = 100
12-3-4+5*6+7*8+9 = 100
12-3-4+5*6-7+8*9 = 100
12*3-4+5-6+78-9 = 100
12*3-4-5-6+7+8*9 = 100
12*3-4*5+67+8+9 = 100
12/3+4*5-6-7+89 = 100
12/3+4*5*6-7-8-9 = 100
12/3+4*5*6*7/8-9 = 100
12/3/4+5*6+78-9 = 100
1+234-56-7-8*9 = 100
1+234*5*6/78+9 = 100
1+234*5/6-7-89 = 100
1+23-4+56+7+8+9 = 100
1+23-4+56/7+8*9 = 100
1+23-4+5+6+78-9 = 100
1+23-4-5+6+7+8*9 = 100
1+23*4+56/7+8-9 = 100
1+23*4+5-6+7-8+9 = 100
1+23*4-5+6+7+8-9 = 100
1+2+34-5+67-8+9 = 100
1+2+34*5+6-7-8*9 = 100
1+2+3+4+5+6+7+8*9 = 100
1+2+3-45+67+8*9 = 100
1+2+3-4+5+6+78+9 = 100
1+2+3-4*5+6*7+8*9 = 100
1+2+3*4-5-6+7+89 = 100
1+2+3*4*56/7-8+9 = 100
1+2+3*4*5/6+78+9 = 100
1+2-3*4+5*6+7+8*9 = 100
1+2-3*4-5+6*7+8*9 = 100
1+2*34-56+78+9 = 100
1+2*3+4+5+67+8+9 = 100
1+2*3+4*5-6+7+8*9 = 100
1+2*3-4+56/7+89 = 100
1+2*3-4-5+6+7+89 = 100
1+2*3*4*5/6+7+8*9 = 100
1-23+4*5+6+7+89 = 100
1-23-4+5*6+7+89 = 100
1-23-4-5+6*7+89 = 100
1-2+3+45+6+7*8-9 = 100
1-2+3*4+5+67+8+9 = 100
1-2+3*4*5+6*7+8-9 = 100
1-2+3*4*5-6+7*8-9 = 100
1-2-34+56+7+8*9 = 100
1-2-3+45+6*7+8+9 = 100
1-2-3+45-6+7*8+9 = 100
1-2-3+45-6-7+8*9 = 100
1-2-3+4*56/7+8*9 = 100
1-2-3+4*5+67+8+9 = 100
1-2*3+4*5+6+7+8*9 = 100
1-2*3-4+5*6+7+8*9 = 100
1-2*3-4-5+6*7+8*9 = 100
1*234+5-67-8*9 = 100
1*23+4+56/7*8+9 = 100
1*23+4+5+67-8+9 = 100
1*23-4+5-6-7+89 = 100
1*23-4-56/7+89 = 100
1*23*4-56/7/8+9 = 100
1*2+34+56+7-8+9 = 100
1*2+34+5+6*7+8+9 = 100
1*2+34+5-6+7*8+9 = 100
1*2+34+5-6-7+8*9 = 100
1*2+34-56/7+8*9 = 100
1*2+3+45+67-8-9 = 100
1*2+3+4*5+6+78-9 = 100
1*2+3-4+5*6+78-9 = 100
1*2+3*4+5-6+78+9 = 100
1*2-3+4+56/7+89 = 100
1*2-3+4-5+6+7+89 = 100
1*2-3+4*5-6+78+9 = 100
1*2*34+56-7-8-9 = 100
1*2*3+4+5+6+7+8*9 = 100
1*2*3-45+67+8*9 = 100
1*2*3-4+5+6+78+9 = 100
1*2*3-4*5+6*7+8*9 = 100
1*2*3*4+5+6+7*8+9 = 100
1*2*3*4+5+6-7+8*9 = 100
1*2*3*4-5-6+78+9 = 100
1*2/3+4*5/6+7+89 = 100
1/2*34-5+6-7+89 = 100
1/2*3/4*56+7+8*9 = 100
1/2/3*456+7+8+9 = 100
Потом я решил просмотреть полную зависимость числа возможных решений таких разложений от всех возможных сумм, в том числе и нецелых. Для этого цикл стал функцией, работающей на заполнение словаря:
Copy Source | Copy HTML
figure = {}
xlist = []
ylist = []
def func():
for n in range(int('44444444', 5)):
num = to_new_base(n, 5)
expr = ''
for i, j in zip(line, num):
expr += i + d[j]
expr += '9'
num_sum = eval(expr)
if num_sum in figure:
figure[num_sum] += 1
else:
figure[num_sum] = 1
for key in sorted(figure):
xlist.append(key)
ylist.append(figure[key])
Списки зависимости ylist=f(xlist) рисуются с помощью matplotlib. Зависимость имеет пик в нуле со 167 решениями:

Левая ветвь не симметрична правой, потому что перед вариантом 1*2*3*4*5*6*7*8*9 по условию задачи минус мы поставить не можем. Чем ближе к нулю, тем чаще встречаются действительные числа, которые можно представить несколькими возможными способами.




Отдельное рассмотрение для решений в области [-1.1, 1.1]: наибольшее число решений приходится, собственно, на ноль, потом на целые числа -1, 1, потом на полуцелые -0.5, 0.5.

Проверено, что любое из целых чисел от 0 до 100 может быть выражено таким способом:

Может быть, эта задача понравится и просто, чтобы задать кому-то, например собственному ребенку или приятелю, на скорость счета и умение обращаться с числами, как когда-то мне она была задана в начальной школе и нужно было найти одно решение, хотя, как я теперь вижу, их было намного больше. А можете попробовать сами в уме или на бумаге найти хотя бы одно из 167 решений для нуля.
30.11.1999 00:00+0300
