Песочница →
Использование инерциальной навигационной системы (ИНС) с несколькими датчиками на примере задачи стабилизации высоты квадрокоптера
В данной статье я постараюсь рассказать о своем опыте создания и реализации алгоритма для обработки сигналов с нескольких стандартных датчиков, входящих в состав ИНС (в английской версии IMU), для решения задачи стабилизации высоты многороторного летательного аппарата (в моем случае — квадрокоптера). На хабре уже был ряд статей, описывающих, что это за игрушка и как её сделать самому. Как программисту по профессии, мне было интересно не только его собрать, но и поковыряться в «мозгах» и сделать что-то полезное для сообщества. В качестве «мозгов» я выбрал Arduino и замечательный проект MultiWii. Он полностью открытый, динамично развивается, но в нем пока есть «белые пятна». Например, неудовлетворительно работает стабилизация положения по высоте. И я решил разобраться, можно ли с имеющимся оборудованием улучшить эту часть системы.
Для начала немного вводной информации, чтобы прояснить, с чем предстоит иметь дело.
Мультиротор — аппарат с несколькими (3, 4, 6, 8) моторами с пропеллерами, каждый из которых создает вертикальную регулируемую тягу. В отличие от вертолета, стабилизация тут полностью электронная, и занимается ей микропроцессор при помощи ИНС (полетный контроллер).
На данный момент в легкой доступности имеем стандартный набор сенсоров:
Такой набор в сборе с Arduino-подобным процессором или в виде отдельной платки можно найти за сумму 70-100$
У каждого датчика свои возможности и слабые стороны. По отдельности ни один из них не может решить ни одну и перечисленных выше задач, поэтому системы ИНС всегда строятся из комбинации датчиков, и самое интересное тут — это вычислительные алгоритмы, позволяющие соединить сильные стороны каждого из датчиков для устранения их недостатков.
Первая задача — стабилизация ориентации — довольно успешно решается гироскопами. Гироскопы очень точно меряют угловую скорость и после интегрирования можно получить углы. Но у них есть проблема — показания уплывают со временем. Для коррекции этого дрифта применяется акселерометр, который всегда (ну или почти всегда в долгосрочной перспективе) знает, где земля. Но акселерометр ничего не почувствует, если его крутить вокруг оси Z, поэтому нам нужен магнетометр, который всегда знает, где север.
Вторая задача — нахождение высоты — частично решается барометром. Если обнулить показания на земле, то при подъеме на каждый метр мы знаем, насколько изменятся его показания (естественно, если мы не летаем 12 часов и не начала меняться погода). Но по условию задачи барометр у нас плохой, и он выдает высоту +-1м с диким шумом амплитудой примерно в этих же пределах. В реальности мой датчик показывает следующее (на 10-й секунде перемещен на 1метр):
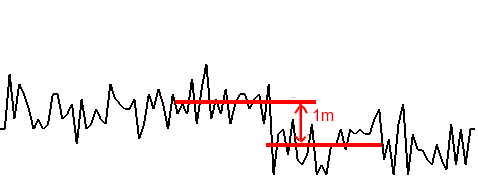
На помощь барометру может прийти сонар, который меряет высоту с очень высокой точностью (даже тот, что я приобрел за 5$, выдает точность ± 3мм по заявлению производителя). Но сонар способен работать только невысоко над землей (2-10м), меряет долго (до 200мс), чувствителен к качеству поверхности, к углу наклона, и может терять сигнал.
Третья задача — определение координат — не решается никак указанными выше датчиками. Акселерометр в комбинации с гироскопом может выдать линейные горизонтальные ускорения, но тут есть две проблемы: постоянно действующий огромный (по сравнению с тем, что будем измерять) вектор 1G, и отсутствие привязок для коррекции. Так что определение координат остается прерогативой GPS-сенсора, и на высокую точность тут рассчитывать не приходится.
Во всех любительских полетных контроллерах задача нахождения ориентации решена хорошо и на ней останавливаться не буду. Задача довольно простая и расписана в интернете (один, два). В MultiWii используется красивое решение без сложностей типа кватернионов и матриц DCM (не забываем, что считать все это будет простенький 16-Мегагерцовый процессор), на основе упрощений для малых углов и комплементарного фильтра.
Итак, ориентацию аппарата в пространстве мы знаем с высокой степенью точности. Теперь можно перейти к основной теме статьи, т. е. постараться улучшить результаты, которые выдает барометр (или сонар), чтобы их можно было скормить ПИД-регулятору. Для этого показания должны поступать без задержек, быть точными в короткой перспективе и не сильно уплывать со временем. Тема ПИД-регуляторов заслуживает отдельного пристального изучения, так как он широко используются в системах управления процессами. Я рекомендую сначала ознакомиться с их определением, чтобы лучше понять рассуждения, изложенные ниже.
Чем нам не подходят показания барометра в текущем виде? Ну во первых, сильная зашумленность сигнала будет вызывать лишние управляющие воздействия на моторы. Применив фильтр низких частот, мы уменьшим шум, но потеряем быстроту измерения. А это значит, что любые кратковременные возмущения останутся без внимания, резкие возмущения отработаются с большой задержкой, и самое главное, мы не получим дифференциальную составляющую (D) для ПИД-регулятора. А как следует из теории, регулятор без этой составляющей склонен к слабозатухающим осцилляциям вокруг целевой величины, что и наблюдается на практике.
Хорошо, оставим барометр и возьмем акселерометр. Вроде все просто — из значения по оси Z вычтем константу 1G, получим линейное вертикальное ускорение. Дважды проинтегрируем его (фактически просуммируем в измерительном цикле) и получим скорость и относительное смещение. Для ПИД-регулятора это лакомые показатели, с ними можно построить хорошую динамическую модель. Но и тут не все так хорошо, как хотелось бы. Наклон аппарата вызовет изменение проекции вектора ускорения А на ось Z. Вибрации от мотора или изменение температуры могут вызвать «сдвиг» чувствительности, и наша константа 1G уже не будет соответствовать реальности. Но даже в случае идеально неподвижного аппарата и точно выставленной 1G, любой сенсор выдает шум. А ведь даже крохотная ошибка в течение десятка секунд двойного интегрирования вырастает до размера слона, и вот мы видим скорость 10м/с и высоту 20м (хотя от земли ещё даже не оторвались).
Если объяснять по простому — этот фильтр применяется к двум величинам, измеряемых разными датчиками, и корректирует одну из них так, что она медленно стремится ко второй. В измерительном цикле фильтр реализуется простой формулой:
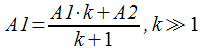
При этом влияние величины A2 на A1 пропорционально разнице между ними и определяется коэффициентом k (чем больше, тем слабее влияние).
Если применить этот фильтр к высоте, найденной акселерометром, и показаниям барометра, получится интересная штука: дрифт акселерометра будет постоянно корректироваться барометром, а показания барометра будут сглаживаться (так как для A2 этот фильтр работает как фильтр низких частот). Но корректироваться будет только второй интеграл, а первый по прежнему спокойно «дрейфовать» в бесконечность, и в итоге из-за малого коэффициента k барометр просто не сможет повлиять на ситуацию.
Почему этот фильтр прекрасно работает для пары гироскоп + акселерометр? Потому что там мы корректируем первый интеграл, и он в конце концов перестает «уплывать», когда величина коррекции за время одного цикла сравняется с величиной ошибки гироскопа, прибавляемой в этом же цикле при интегрировании.
Но и из пары барометр+акселерометр можно извлечь нечто полезное, если применить к ним ПИД-регулятор (да-да, область их применения крайне обширна).
Итак, в чем главное слабое место нашего интегратора ускорения? В микро-ошибке, которая может возникнуть по разным причинам, описанным выше, при вычитании константы 1G. Если записать искомое ускорение в виде:

то, регулируя величину bias, можно управлять и первым интегралом (скоростью), и вторым (смещением). Итак, цель нашего ПИД-регулятора найдена. Но надо ещё знать ошибку. Сделаем допущение, что bias зафиксируется после наступлении некоей стабилизации параметров системы (температурных, вибрационных и т. д.). Когда bias будет найден, показания акселерометра станут очень близки к истине и можно применить комплементарный фильтр, скрестив их с барометром. Величина коррекции этого фильтра и будет ошибкой, от которой будет отталкиваться ПИД-регулятор (он стремится свести ошибку к 0 за счет регулирования целевой переменной).
Дальше находим все три составляющие ПИД-регулятора. Пропорциональная (P) — это сама ошибка. Интегральная (I) — просто интегрируем её. Дифференциальная (D) — по теории надо дифференцировать ошибку. Но в ней сидят ужасные шумы барометра и акселерометра. Такое дифференцировать страшно, поэтому применим хитрость — возьмем за D-составляющую найденную акселерометром скорость с отрицательным знаком. Так как D призвана ввести затухание в регулятор, скорость тут вполне сгодится — чем она больше, тем больше надо её «погасить».
Умножим каждый из компонентов на свои коэффициенты, сложим и получим bias. Но тут применим вторую хитрость — не будем прибавлять bias напрямую к ускорению, а прибавим только I-часть. Именно она описывает величину постоянно действующей ошибки, что соответствует нашему допущению о медленном изменении bias.
P и D части прибавим к скорости, умножив на dT (так как позаимствовали их из ускорения).
Так как основная задача регулятора — найти постоянную составляющую ошибки, я решил настроить его достаточно «мягко», чтобы по минимуму влиять на кратковременные изменения. Но тут остается широкое поле для экспериментов, и все буде определяться поведением реальных датчиков.
Выше я упомянул, что для определения высоты нам понадобится ещё и гироскоп. Действительно, описанный выше алгоритм будет работать, только если вектор A (в локальной системе) смотрит точно вдоль оси Z. Как только аппарат наклонится, произойдут две неприятные вещи: проекция A на ось Z изменится и ПИД-регулятор начнет заново медленно и мучительно искать bias. И вторая — любое горизонтальное ускорение начнет давать ненулевую проекцию на локальную ось Z. При углах наклона в 45° уже и не поймешь, где какое ускорение.
Но так как мы знаем точную ориентацию локальной системы относительно глобальной, нет ничего сложного восстановить справедливость — просто спроектируем локальный вектор A на локальный вектор G (изначально найденный акселерометром и заботливо вращаемый гироскопом), который всегда смотрит в землю.
Операция эта простая и вытекает из определения векторного произведения:
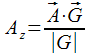
Сделать это надо до вычитания 1G.
Теперь можно посмотреть на код и результаты.
Данные сенсоров приходят в следующих переменных:
EstG.V – вектор G (он получен ранее при нахождении ориентации)
accADC – чистые данные с акселерометра
BaroAlt – данные с барометра, конвертированные в cm
На выходе получаем accZ, vel, alt.
Как видно, вычислительная сложность алгоритма довольно простая и Arduino его «переварит» легко (особенно если перевести в целочисленную арифметику, но тогда код станет плохо читаем).
PS: в видео есть фраза об отключении алгоритма при определенном угле наклона, и и-за этого возникает выброс ошибки. На самом деле это ограничение не нужно — алгоритм работает стабильно при любом угле от 0° до 360°
Если к этому алгоритму подключить сонар (вмето BaroAlt взять SonarAlt), то кривая высоты выглядит практически идеально. Таким образом, на низкой высоте используем сонар, при появлении ошибок или близко к пределу измерений переключаемся на барометр (предварительно согласовав высоты в период поступления достоверных данных с сонара).
К сожалению, погода пока не дает провести полетные испытания нового алгоритма. Как только появятся результаты, выложу графики сонара, отлаженный исходный код всего проекта и полетное видео.
Для начала немного вводной информации, чтобы прояснить, с чем предстоит иметь дело.
Мультиротор — аппарат с несколькими (3, 4, 6, 8) моторами с пропеллерами, каждый из которых создает вертикальную регулируемую тягу. В отличие от вертолета, стабилизация тут полностью электронная, и занимается ей микропроцессор при помощи ИНС (полетный контроллер).
Какие задачи необходимо решать в полете?
- Определение ориентации (углов по трем осям относительно земли) и стабилизация по ним
- Определение высоты и стабилизация по ней
- Определение координат и полет по заданным точкам
- Прием команд с пульта управления и выдача управляющих сигналов на моторы
Что мы имеем в распоряжении?
На данный момент в легкой доступности имеем стандартный набор сенсоров:
- довольно хорошие 3-х осевые гироскопы.
- средние по качеству 3-х осевые акселерометры
- средний по качеству 3-х осевой магнетометр
- средний или плохой барометр
Такой набор в сборе с Arduino-подобным процессором или в виде отдельной платки можно найти за сумму 70-100$
У каждого датчика свои возможности и слабые стороны. По отдельности ни один из них не может решить ни одну и перечисленных выше задач, поэтому системы ИНС всегда строятся из комбинации датчиков, и самое интересное тут — это вычислительные алгоритмы, позволяющие соединить сильные стороны каждого из датчиков для устранения их недостатков.
Первая задача — стабилизация ориентации — довольно успешно решается гироскопами. Гироскопы очень точно меряют угловую скорость и после интегрирования можно получить углы. Но у них есть проблема — показания уплывают со временем. Для коррекции этого дрифта применяется акселерометр, который всегда (ну или почти всегда в долгосрочной перспективе) знает, где земля. Но акселерометр ничего не почувствует, если его крутить вокруг оси Z, поэтому нам нужен магнетометр, который всегда знает, где север.
Вторая задача — нахождение высоты — частично решается барометром. Если обнулить показания на земле, то при подъеме на каждый метр мы знаем, насколько изменятся его показания (естественно, если мы не летаем 12 часов и не начала меняться погода). Но по условию задачи барометр у нас плохой, и он выдает высоту +-1м с диким шумом амплитудой примерно в этих же пределах. В реальности мой датчик показывает следующее (на 10-й секунде перемещен на 1метр):

На помощь барометру может прийти сонар, который меряет высоту с очень высокой точностью (даже тот, что я приобрел за 5$, выдает точность ± 3мм по заявлению производителя). Но сонар способен работать только невысоко над землей (2-10м), меряет долго (до 200мс), чувствителен к качеству поверхности, к углу наклона, и может терять сигнал.
Третья задача — определение координат — не решается никак указанными выше датчиками. Акселерометр в комбинации с гироскопом может выдать линейные горизонтальные ускорения, но тут есть две проблемы: постоянно действующий огромный (по сравнению с тем, что будем измерять) вектор 1G, и отсутствие привязок для коррекции. Так что определение координат остается прерогативой GPS-сенсора, и на высокую точность тут рассчитывать не приходится.
Во всех любительских полетных контроллерах задача нахождения ориентации решена хорошо и на ней останавливаться не буду. Задача довольно простая и расписана в интернете (один, два). В MultiWii используется красивое решение без сложностей типа кватернионов и матриц DCM (не забываем, что считать все это будет простенький 16-Мегагерцовый процессор), на основе упрощений для малых углов и комплементарного фильтра.
Итак, ориентацию аппарата в пространстве мы знаем с высокой степенью точности. Теперь можно перейти к основной теме статьи, т. е. постараться улучшить результаты, которые выдает барометр (или сонар), чтобы их можно было скормить ПИД-регулятору. Для этого показания должны поступать без задержек, быть точными в короткой перспективе и не сильно уплывать со временем. Тема ПИД-регуляторов заслуживает отдельного пристального изучения, так как он широко используются в системах управления процессами. Я рекомендую сначала ознакомиться с их определением, чтобы лучше понять рассуждения, изложенные ниже.
Сглаживаем
Чем нам не подходят показания барометра в текущем виде? Ну во первых, сильная зашумленность сигнала будет вызывать лишние управляющие воздействия на моторы. Применив фильтр низких частот, мы уменьшим шум, но потеряем быстроту измерения. А это значит, что любые кратковременные возмущения останутся без внимания, резкие возмущения отработаются с большой задержкой, и самое главное, мы не получим дифференциальную составляющую (D) для ПИД-регулятора. А как следует из теории, регулятор без этой составляющей склонен к слабозатухающим осцилляциям вокруг целевой величины, что и наблюдается на практике.
Интегрируем
Хорошо, оставим барометр и возьмем акселерометр. Вроде все просто — из значения по оси Z вычтем константу 1G, получим линейное вертикальное ускорение. Дважды проинтегрируем его (фактически просуммируем в измерительном цикле) и получим скорость и относительное смещение. Для ПИД-регулятора это лакомые показатели, с ними можно построить хорошую динамическую модель. Но и тут не все так хорошо, как хотелось бы. Наклон аппарата вызовет изменение проекции вектора ускорения А на ось Z. Вибрации от мотора или изменение температуры могут вызвать «сдвиг» чувствительности, и наша константа 1G уже не будет соответствовать реальности. Но даже в случае идеально неподвижного аппарата и точно выставленной 1G, любой сенсор выдает шум. А ведь даже крохотная ошибка в течение десятка секунд двойного интегрирования вырастает до размера слона, и вот мы видим скорость 10м/с и высоту 20м (хотя от земли ещё даже не оторвались).
Комплементарный фильтр
Если объяснять по простому — этот фильтр применяется к двум величинам, измеряемых разными датчиками, и корректирует одну из них так, что она медленно стремится ко второй. В измерительном цикле фильтр реализуется простой формулой:
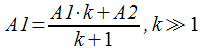
При этом влияние величины A2 на A1 пропорционально разнице между ними и определяется коэффициентом k (чем больше, тем слабее влияние).
Если применить этот фильтр к высоте, найденной акселерометром, и показаниям барометра, получится интересная штука: дрифт акселерометра будет постоянно корректироваться барометром, а показания барометра будут сглаживаться (так как для A2 этот фильтр работает как фильтр низких частот). Но корректироваться будет только второй интеграл, а первый по прежнему спокойно «дрейфовать» в бесконечность, и в итоге из-за малого коэффициента k барометр просто не сможет повлиять на ситуацию.
Почему этот фильтр прекрасно работает для пары гироскоп + акселерометр? Потому что там мы корректируем первый интеграл, и он в конце концов перестает «уплывать», когда величина коррекции за время одного цикла сравняется с величиной ошибки гироскопа, прибавляемой в этом же цикле при интегрировании.
ПИД-регулятор приходит на помощь
Но и из пары барометр+акселерометр можно извлечь нечто полезное, если применить к ним ПИД-регулятор (да-да, область их применения крайне обширна).
Итак, в чем главное слабое место нашего интегратора ускорения? В микро-ошибке, которая может возникнуть по разным причинам, описанным выше, при вычитании константы 1G. Если записать искомое ускорение в виде:

то, регулируя величину bias, можно управлять и первым интегралом (скоростью), и вторым (смещением). Итак, цель нашего ПИД-регулятора найдена. Но надо ещё знать ошибку. Сделаем допущение, что bias зафиксируется после наступлении некоей стабилизации параметров системы (температурных, вибрационных и т. д.). Когда bias будет найден, показания акселерометра станут очень близки к истине и можно применить комплементарный фильтр, скрестив их с барометром. Величина коррекции этого фильтра и будет ошибкой, от которой будет отталкиваться ПИД-регулятор (он стремится свести ошибку к 0 за счет регулирования целевой переменной).
Дальше находим все три составляющие ПИД-регулятора. Пропорциональная (P) — это сама ошибка. Интегральная (I) — просто интегрируем её. Дифференциальная (D) — по теории надо дифференцировать ошибку. Но в ней сидят ужасные шумы барометра и акселерометра. Такое дифференцировать страшно, поэтому применим хитрость — возьмем за D-составляющую найденную акселерометром скорость с отрицательным знаком. Так как D призвана ввести затухание в регулятор, скорость тут вполне сгодится — чем она больше, тем больше надо её «погасить».
Умножим каждый из компонентов на свои коэффициенты, сложим и получим bias. Но тут применим вторую хитрость — не будем прибавлять bias напрямую к ускорению, а прибавим только I-часть. Именно она описывает величину постоянно действующей ошибки, что соответствует нашему допущению о медленном изменении bias.
P и D части прибавим к скорости, умножив на dT (так как позаимствовали их из ускорения).
Так как основная задача регулятора — найти постоянную составляющую ошибки, я решил настроить его достаточно «мягко», чтобы по минимуму влиять на кратковременные изменения. Но тут остается широкое поле для экспериментов, и все буде определяться поведением реальных датчиков.
А как же гироскоп?
Выше я упомянул, что для определения высоты нам понадобится ещё и гироскоп. Действительно, описанный выше алгоритм будет работать, только если вектор A (в локальной системе) смотрит точно вдоль оси Z. Как только аппарат наклонится, произойдут две неприятные вещи: проекция A на ось Z изменится и ПИД-регулятор начнет заново медленно и мучительно искать bias. И вторая — любое горизонтальное ускорение начнет давать ненулевую проекцию на локальную ось Z. При углах наклона в 45° уже и не поймешь, где какое ускорение.
Но так как мы знаем точную ориентацию локальной системы относительно глобальной, нет ничего сложного восстановить справедливость — просто спроектируем локальный вектор A на локальный вектор G (изначально найденный акселерометром и заботливо вращаемый гироскопом), который всегда смотрит в землю.
Операция эта простая и вытекает из определения векторного произведения:
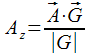
Сделать это надо до вычитания 1G.
Теперь можно посмотреть на код и результаты.
#define ACC_BARO_CMPF 300.0f
#define ACC_BARO_P 30.0f
#define ACC_BARO_I (ACC_BARO_P * 0.001f)
#define ACC_BARO_D (ACC_BARO_P * 0.001f)
#define VEL_SCALE ((1.0f — 1.0f/ACC_BARO_CMPF)/1000000.0f)
#define ACC_SCALE 9.80665f / acc_1G / 10000.0f
err = (alt - BaroAlt)/ACC_BARO_CMPF; // P term of error
errI+= err * ACC_BARO_I; // I term of error
accZ = (accADC[0]*EstG.V.X + accADC[1]*EstG.V.Y + accADC[2]*EstG.V.Z) *
InvSqrt(fsq(EstG.V.X) + fsq(EstG.V.Y) + fsq(EstG.V.Z))
- errI - acc_1G;
// Integrator - velocity, cm/sec
vel+= (accZ - err*ACC_BARO_P - vel*ACC_BARO_D) * cycleTime * ACC_SCALE;
// Integrator - altitude, cm
alt+= vel * cycleTime * VEL_SCALE;
// Apply ACC->BARO complementary filter
alt-= err;
errPrev = err;Данные сенсоров приходят в следующих переменных:
EstG.V – вектор G (он получен ранее при нахождении ориентации)
accADC – чистые данные с акселерометра
BaroAlt – данные с барометра, конвертированные в cm
На выходе получаем accZ, vel, alt.
Как видно, вычислительная сложность алгоритма довольно простая и Arduino его «переварит» легко (особенно если перевести в целочисленную арифметику, но тогда код станет плохо читаем).
PS: в видео есть фраза об отключении алгоритма при определенном угле наклона, и и-за этого возникает выброс ошибки. На самом деле это ограничение не нужно — алгоритм работает стабильно при любом угле от 0° до 360°
Если к этому алгоритму подключить сонар (вмето BaroAlt взять SonarAlt), то кривая высоты выглядит практически идеально. Таким образом, на низкой высоте используем сонар, при появлении ошибок или близко к пределу измерений переключаемся на барометр (предварительно согласовав высоты в период поступления достоверных данных с сонара).
К сожалению, погода пока не дает провести полетные испытания нового алгоритма. Как только появятся результаты, выложу графики сонара, отлаженный исходный код всего проекта и полетное видео.
06.02.2012 04:24+0400
