algorithm →
Построение цифрового фильтра с конечной импульсной характеристикой
Вступление издалека
Недавно передо мной встала достаточно интересная задача, с которой я раньше никогда не сталкивался — борьба с шумом. Мы принимали сигнал с датчиков на аналогово-цифровой преобразователь (АЦП)
А так как данная тема для меня была (хотя и сейчас есть кое-где) темным лесом, я пошел мучить вопросами гугл, мне показалось освящена эта тема не очень подробно и доступно, поэтому решил написать статью с примером разработки и готовым исходником.
Ближе к делу
Цифровые фильтры могут быть двух видов – с конечной и с бесконечной импульсной характеристикой (КИХ и БИХ). Для решения моей задачи подходит КИХ-фильтр, поэтому про него и расскажу.
Работает фильтр довольно просто: фильтр получает значения, с помощью коэффициентов преобразует их и выдаёт выходную последовательность, тогда с формулой самого фильтра всё понятно:

Она реализуется через цикл, но постойте, а где же взять нужные коэффициенты? Вот тут-то как раз и зарыта собака (и не одна).
Параметры фильтра
Естественно для разных фильтров нужны разные коэффициенты, и для этого нужно определиться с параметрами фильтра, это обычно сначала делается теоретически (с умным видом прикидываем какая у нашего сигнала частота, потом частоты, которые надо отсеивать), а потом изучаем АЧХ реальных измерений (и осознаем, как сильно мы ошибались).
По этим АЧХ мы определяемся с идеальной частотной характеристикой (какие частоты проходят свободно, какие мы убираем и как сильно), теперь нам нужна идеальная импульсная характеристика её можно посчитать как Фурье-образ от идеальной частотной:

где H_D(w) – идеальная характеристика.
Но можно пойти и по более простому пути – есть уже заранее вычисленные идеальные импульсные характеристики, например для фильтра нижних частот формула выглядит следующим образом:
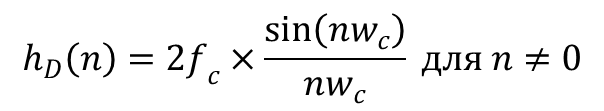
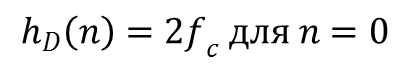
где fc и wc – частота среза.
Итак, осталось уже немного идеал идеалом, а мы имеем дело с практикой, и нам нужна «реальная» импульсная характеристика. Для её расчета нам понадобится весовая функция w(n), их есть несколько разновидностей, в зависимости от требований к фильтру (Хэмминга, Хеннинга, Блэкмена, Кайзера, о них не говорю, ибо статья и так большая), в нашем случае я использую функцию Блэкмена:
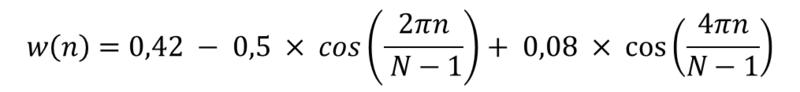
где N – длина фильтра, т.е. количество коэффициентов.
Теперь надо перемножить идеальную импульсную характеристику и весовую функцию:
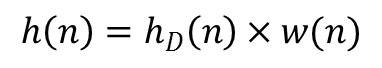
Финишная прямая
Теперь мы готовы рассчитать выходные значения, по формуле фильтра, она самая первая в этой статье, ну вот и всё, в завершение привожу исходный код фильтра:
void Filter (const double in[], double out[], int sizeIn)
{
const int N = 20; //Длина фильтра
long double Fd = 2000; //Частота дискретизации входных данных
long double Fs = 20; //Частота полосы пропускания
long double Fx = 50; //Частота полосы затухания
long double H [N] = {0}; //Импульсная характеристика фильтра
long double H_id [N] = {0}; //Идеальная импульсная характеристика
long double W [N] = {0}; //Весовая функция
//Расчет импульсной характеристики фильтра
double Fc = (Fs + Fx) / (2 * Fd);
for (int i=0;i<N;i++)
{
if (i==0) H_id[i] = 2*M_PI*Fc;
else H_id[i] = 2*sinl(2*M_PI*Fc*i )/(2*M_PI*i);
//else H_id[i] = ( sin( 2*M_PI*Fc*(i-N/2) ) ) /((i-N/2));
// весовая функция Блекмена
W [i] = 0.42 - 0.5 * cosl((2*M_PI*i) /( N-1)) + 0.08 * cosl((4*M_PI*i) /( N-1));
H [i] = H_id[i] * W[i];
}
//Нормировка импульсной характеристики
double SUM=0;
for (int i=0; i<N; i++) SUM +=H[i];
for (int i=0; i<N; i++) H[i]/=SUM; //сумма коэффициентов равна 1
//Фильтрация входных данных
for (int i=0; i<sizeIn; i++)
{
out[i]=0.;
for (int j=0; j<N-1; j++)// та самая формула фильтра
out[i]+= H[j]*in[i-j];
}
}При подготовке статьи использовались:
Основные характеристики и параметры фильтров. analogiu.ru/6/6-5-2.html
Айфичер Э. Джервис Б. Цифровая обработка сигналов. Практический подход. 2-е издание
11.09.2011 09:31+0400
