орбита
Найдено: 1 запись
Научно популярное →
О современных методах околоземной астрономии
Вступление лирическое
Если бы античный человек попал в наше время и взглянул на ночное небо, он бы наверное начал немедленно молиться своим богам, а может быть подумал, что пришёл судный день. Для нас, людей, чьё небо скрыто за световым загрязнением городов и деревень, такое утверждение может показаться абсурдным: «Звёзды такие же звёзды, что с них взять то?». Но если разобраться — оно обретёт смысл.

Выйдете вечером на природу и посмотрите в небо. Ничего не видите? Смотрите внимательнее! Практически в любой момент по небу будут лететь 2-3 ярких точки, а если присмотреться, то можно найти ещё с пяток более медленных и тусклых. Иногда (раза 3-4 за ночь) вам может посчастливиться и вы увидите ярчайшую вспышку на небе, лишь луна сравниться с ней по яркости. Всё это достижения человеческого прогресса — спутники. Для античного человека, для которого небо было символом постоянности, которое он видит над собой из ночи в ночь всё это мельтешение было бы воспринято как что-то противоестественное.
Вступление прагматическое
Хаброюзер — он не античный человек и в звёздах в большинстве своём не разбирается. И даже если воспользуется специальным софтом и литературой , то научиться разбираться на уровне древних ему потребуется не одна неделя втыкания в небо и зубрёжки античных легенд. Но, Хаброюзер, — он человек современный, технически подкованный и в своём большинстве разбирается в науке. А это значит, что среди древних он бы смог прослыть мудрецом — предсказателем, умеющим предсказывать появление этих новомодных летающих звёзд. Если бы знал, как это сделать. А вот именно о том как это сегодня делается я тут и расскажу.
Введение
Всё, что я тут буду писать это достаточно известные алгоритмы, многие из которых используются в других проблемах. Большинство астрономов с ними так или иначе знакомы, а особо продвинутые даже знают как их использовать. Для этих людей, иже они будут читать сей опус, сразу оговорюсь: среди множества всех алгоритмов я выбираю те, которые на мой взгляд наиболее просты и наиболее интересны. Если вы предложите какую-то из частей переписать более просто/интересно — я с удовольствием размещу вашу версию. Так же, сразу оговорюсь, что всё, что тут находится относится именно к «Научно-популярному», вдаваться в глубины матана я не буду. Тем, кому не интересна научно-популярная часть, можете сразу перейти к концовке, там список программ с которыми можно поиграть.
Задача прогнозирования траектории спутников появилась ещё давным-давно, с запуском первого спутника. Но в те времена нельзя было ещё точно предположить влияющие на полёт факторы, поэтому прогнозирование было грубым. Но со временем эта наука развилась и была способна создать такие системы, как GPS, которые позиционируют вас с точностью до нескольких метров.
Других научно-популярных статей по тематике я не видел не на хабре нигде в других местах. Хотя специализированной инфы полно. А так как на компе валялись заготовки для одной методички, решил имеющуюся там инфу упростить, структурировать и выложить тут.
Основы
Наверняка, ещё в школе вам рассказали, что тела притягиваются друг к другу с силой:

Где m1, m2 — массы тел, а r — расстояние между ними. Я вас разочарую. В реальности этого обычно недостаточно. Конечно, каждый атом, находящийся в первом теле притягивает каждый атом второго тела именно по этой формуле. Результирующая этих сил не обязательно вычимсляется именно по этой формуле. Тела же могут иметь разную плотность, да и их форма может отличатся от идеальной сферы. Формула справедлива только если тела удалены друг от друга на расстояние r>>l, где l — линейные размеры тел. В случае, если расстояние до тела сравнимо с его размерами этот способ не может применяться для точных расчетов: поверхности Земли величина свободного ускорения g не постоянна и изменяется на пару процентов. Обходится эта проблема несколькими способами, которые сводятся приближению распределения масс Земли моделью.
Модели Земли
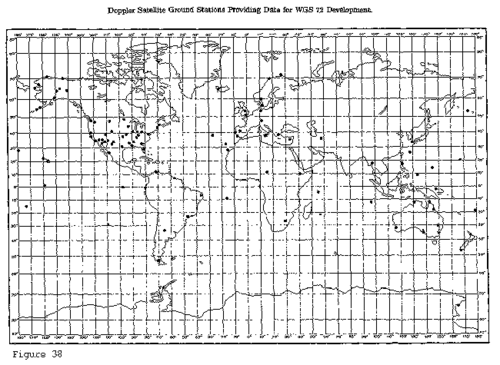
Здесь я расскажу о двух самых классических моделях. Первая — задать Землю суммой точечных масс, положительных или отрицательных, распределённых по поверхности. Обычно эту модель используют для построения траектории взлетающих ракет, так как модель даёт неплохую точность в окрестности Земли. На большой высоте этот метод может дать достаточную точность при большом количестве вычислений, что считается неприемлемым.
Второй способ чуть более сложен математически, зато даёт хорошие результаты на всём пространстве высот, кроме самых низких. Основан он на матане, который зовётся "сферические функции", но по сути имеет простое объяснение. Пусть у нас есть функция гравитационного потенциала в каждой точке пространства:

Где
20.08.2011 02:56+0400
