Подсознание →
Программирование в таблицах — новая концепция записи условных (и не только) конструкций
Не так давно, в процессе поиска в сети альтернативных подходов к программированию я наткнулся на очень интересное видео. Это 40-минутная презентация с интригующим названием «No Ifs, Ands, or Buts. Uncovering the Simplicity of Conditionals». Автор презентации Джонатан Эдвардс (Jonathan Edwards) рассказывает о новой концепции записи условных конструкций при помощи созданных им схематических таблиц (schematic tables).
Эта тема должна быть интересна всем, кто хоть немного интересуется программированием. Если у вас нет в распоряжении лишних сорока минут или вы не можете посмотреть видео по какой-либо другой причине, предлагаю ознакомиться с моим кратким пересказом презентации Джонатана.
Автор оригинальной идеи на простых примерах показывает нам ключевые особенности схематических таблиц и сравнивает их с традиционной записью условных конструкций на языке C (на самом деле Java, но в примерах в основном используется его C-подножество). Кроме видео, на данную тему есть также статья, где концепция описана более формальным языком. Так как данный пересказ нацелен на то, чтобы вкратце поведать вам о самых интересных моментах презентации, я опустил некоторые математические подробности, которыми оперирует автор, и сосредоточился на примерах и сравнениях.
Рассмотрим для начала структуру схематической таблицы на примере функции

В первом столбце записываются переменные. В этом примере у нас их только две — входной параметр
Таким образом, столбцы отвечают за условия. Строки таблицы, в свою очередь, отвечают за действия. Они содержат функции, которые выполняются последовательно одна за другой, начиная сверху и двигаясь вниз. Давайте запишем последовательность действий, определенных в схематической таблице функции
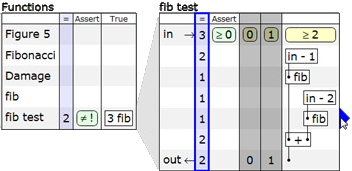
Как видно из рисунка, в качестве входного параметра функции было передано число 3, и она вернула нам 2. Запись в столбце
Возможность просмотра всех промежуточных значений является одной из замечательных особенностей схематических таблиц. Джонатан утверждает, что позаимствовал эту идею у электронных таблиц (spread sheets), в которых все значения вычисляются на лету. Если кликнуть на синюю стрелку, над которой находится курсор на рисунке выше, появится еще одна таблица, соответствующая рекурсивному вызову функции
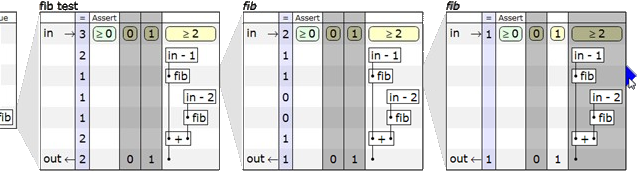
Подобная возможность потенциально может сделать процесс отладки приятным занятием.
Итак, на простом примере мы рассмотрели основные особенности схематической таблицы. Теперь взглянем на пример посложнее, который продемонстрирует нам одно из несомненных преимуществ схематических таблиц.
Попробуем представить условие-переключатель при помощи схематической таблицы. Допустим, мы пишем игру, в которой присутствует метод для вычисления нанесенного урона. Назовем его
Исходный код метода:
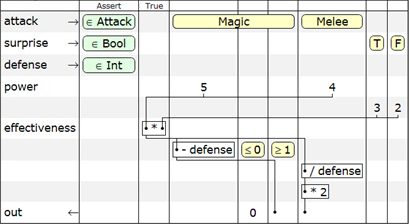
Рассмотрим те элементы таблицы, которые нам еще не встречались. Во-первых, здесь присутствует несколько входящих параметров, каждый из которых принадлежит имеет определенный тип. Во-вторых, после столбца
Итак, двигаясь сверху вниз и размышляя слева направо, мы приходим к такой последовательности действий:
Горизонтальные линии отображают потоки данных между условиями, определенными в таблице. Таким образом, наличие горизонтальной линии всегда свидетельствует об использовании данных, посчитанных в одном условии (или безусловно) в вычислениях с другим условием.
Визуальное сравнение исходного кода метода
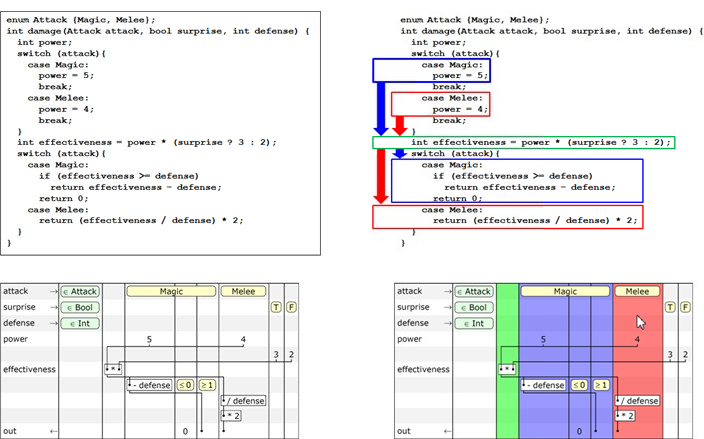
Слева сравнивается размер конструкции на экране при двух различных способах записи, а справа наглядно показано переплетение логики метода. Так как в текстовой записи логики программы присутствует только одно измерение, в нашем примере возникает «пробка» — зеленый участок посередине помещен между двумя условными блоками. Это немного затрудняет восприятие кода, если мы хотим, например, узнать результат выполнения при выполнении условия
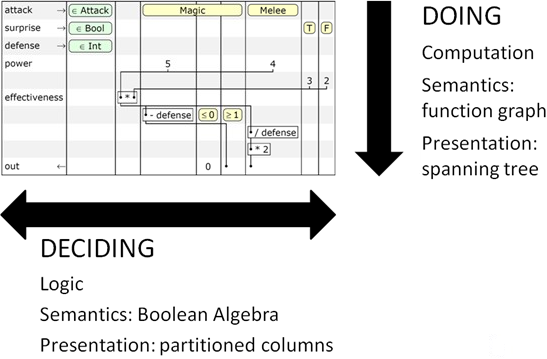
На горизонтальной оси таблицы осуществляется принятие решений. Для записи условий используется семантика булевой алгебры.
На вертикальной оси выполняются действия, которые записываются в виде графа функций, связанных между собой посредством входных параметров и возвращаемых значений.
Если вы все еще скептически относитесь к концепции схематических таблиц, предлагаю вам взглянуть на следующий рисунок.

Оказывается, что такие виды условных конструкций, как вложенные if-then-else условия, switch-выражения и даже полиморфизм (не рассмотренный здесь), — все они сводятся к единому виду при использовании схематических таблиц. На мой взгляд, это хороший знак. Здесь будет уместным привести высказывание Альберта Эйнштейна:
В данной заметке я не рассматривал полиморфизм, так как он не вносит больших изменений в структуру таблицы. Пример того, как заменить перекрытие (overriding) метода на языке Java записью в виде схематической таблицы, начинается на видео презентации с 29-й минуты.
Описанная концепция является одной из нескольких интересных возможностей, положенных в основу разрабатываемого Джонатаном языка программирования Coherence. Скриншоты в статье были сделаны с видео презентации. Автор разработал оболочку, которая предоставляет средства для интерактивной работы со схематическими таблицами, их редактирования и выполнения, а также написания юнит-тестов. Увидеть все это в действии можно на видео. Автор также выложил исходный код оболочки (написанный на С#) вместе с исполняемым файлом для ОС Windows. [скачать]
Дополнительные материалы по теме, включая статью с формальным описанием концепции схематических таблиц, можно найти на сайте www.subtextual.org. У автора также есть блог. Хоть он и редко обновляется, там можно найти описание и других интересных идей, таких как, например, co-actions.
Чтобы лучше понять идеологию Джонатана, можно ознакомиться с его довольно-таки радикальным манифестом, в котором он высказывает доводы против принятой в настоящее время записи логики программы в виде исходного кода и предлагает новые пути развития программирования.
Благодарю за внимание.
UPD:
В комментариях люди высказывают сомнения по поводу целесообразности применения схематических таблиц на практике. Попробую немного прояснить ситуацию.
Данный метод записи логики программы ни в коем случае не позиционируется как завершенная разработка, для которой осталось только написать IDE с компилятором и пустить ее в массы. На данный момент это только концепция. На мой взгляд, она наталкивает на некоторые размышления о текущем положении дел в области программирования. Я решил, что хабрасообществу будет интересно узнать о ней, так как в последнее время из новый веяний в области мы можем наблюдать лишь появление новых языков, которые основываются на уже существующих парадигмах программирования, не смотря на то, что включают в себя механизмы для более простой организации параллельных вычислений.
UPD2:
Прошу прощения за дезинформацию. Исходники оболочки, написанный на C#, и исполняемый файл для ОС Windows можно скачать с сайта проекта, см. первый вопрос в разделе FAQ. Subtext — это ее старое название, сейчас проект носит имя Coherence.
P. S. Если у вас есть замечания по стилю изложения или оформлению статьи, не стесняйтесь писать их в комментариях или мне лично. Я буду рад любой критике.
Эта тема должна быть интересна всем, кто хоть немного интересуется программированием. Если у вас нет в распоряжении лишних сорока минут или вы не можете посмотреть видео по какой-либо другой причине, предлагаю ознакомиться с моим кратким пересказом презентации Джонатана.
Предисловие
Автор оригинальной идеи на простых примерах показывает нам ключевые особенности схематических таблиц и сравнивает их с традиционной записью условных конструкций на языке C (на самом деле Java, но в примерах в основном используется его C-подножество). Кроме видео, на данную тему есть также статья, где концепция описана более формальным языком. Так как данный пересказ нацелен на то, чтобы вкратце поведать вам о самых интересных моментах презентации, я опустил некоторые математические подробности, которыми оперирует автор, и сосредоточился на примерах и сравнениях.
Схематические таблицы
Рассмотрим для начала структуру схематической таблицы на примере функции
fib. Она принимает на вход один параметр n и возвращает число из последовательности Фибоначчи, порядковый номер которого равен значению n. Исходный код функции:int fib(int n) {
assert(n >= 0);
if (n == 0) return 0;
if (n == 1) return 1;
return fib(n - 1)
+ fib(n - 2)
}
* This source code was highlighted with Source Code Highlighter.
В первом столбце записываются переменные. В этом примере у нас их только две — входной параметр
in и возвращаемое значение out. Второй столбец содержит утверждения (Assert). Здесь он используется для проверки неотрицательности входного параметра. Во всех последующих столбцах записываются условия. Первый столбец после Assert считается истинным, когда in == 0, второй — когда n == 1, и третий — при n >= 2.Таким образом, столбцы отвечают за условия. Строки таблицы, в свою очередь, отвечают за действия. Они содержат функции, которые выполняются последовательно одна за другой, начиная сверху и двигаясь вниз. Давайте запишем последовательность действий, определенных в схематической таблице функции
fib:- Если
in < 0, сообщить об ошибке (стандартное поведение при невыполнении условия в столбцеAssert) и завершить выполнение. - Если
in == 0, вернуть 0. - Если
in == 1, вернуть 1. - Если
in >= 2, перейти к следующему пункту. - Передать результат выражения
in - 1в качестве входного параметра в рекурсивный вызовfib. - Передать результат выражения
in - 2во второй рекурсивный вызов функции. - Вернуть результат сложения значений, полученных из обоих рекурсивных вызовов.
Assert записать утверждение, которое должно выполняться, а в следующем за Assert столбце необходимо записать безусловный вызов проверяемой функции, передав ей на вход интересующие нас значения. Результат выполнения функции будет выведен в столбце «=». В нашем случае тест называется fib test.
Как видно из рисунка, в качестве входного параметра функции было передано число 3, и она вернула нам 2. Запись в столбце
Assert значит, что результатом функции не должна быть ошибка. Заметьте, что таблица справа — это та же самая схематическая таблица, которую мы создали для функции fib, только теперь в нее был добавлен еще один столбец с именем «=», в котором для каждой строки записан результат операции, выполняемой в данной строке. Кроме того, серым цветом залиты те столбцы, условия которых не выполнены. В данном случае выполняется условие последнего столбца (3 >= 2), и мы получаем результат сложения значений, полученных из двух рекурсивных вызовов функции fib.Возможность просмотра всех промежуточных значений является одной из замечательных особенностей схематических таблиц. Джонатан утверждает, что позаимствовал эту идею у электронных таблиц (spread sheets), в которых все значения вычисляются на лету. Если кликнуть на синюю стрелку, над которой находится курсор на рисунке выше, появится еще одна таблица, соответствующая рекурсивному вызову функции
fib. Этот процесс можно продолжать и дальше. В каждой следующей таблице мы видим, какой столбец является истинным в текущем вызове, и значения операций, выполняемых в каждой строке таблицы.
Подобная возможность потенциально может сделать процесс отладки приятным занятием.
Итак, на простом примере мы рассмотрели основные особенности схематической таблицы. Теперь взглянем на пример посложнее, который продемонстрирует нам одно из несомненных преимуществ схематических таблиц.
Переключатели (switch-statements)
Попробуем представить условие-переключатель при помощи схематической таблицы. Допустим, мы пишем игру, в которой присутствует метод для вычисления нанесенного урона. Назовем его
damage. На основании типа атаки, ее неожиданности и уровня защиты атакуемого метод возвращает определенное значение урона.Исходный код метода:
enum Attack {Magic, Melee};
int damage(Attack attack, bool surprise, int defense) {
int power;
switch (attack) {
case Magic:
power = 5;
break;
case Melee:
power = 4;
break;
}
int effectiveness = power * (surprise ? 3 : 2);
switch (attack) {
case Magic:
if (effectiveness >= defense)
return effectiveness - defense;
return 0;
case Melee:
return (effectiveness / defense) * 2;
}
}
* This source code was highlighted with Source Code Highlighter.
Рассмотрим те элементы таблицы, которые нам еще не встречались. Во-первых, здесь присутствует несколько входящих параметров, каждый из которых принадлежит имеет определенный тип. Во-вторых, после столбца
Assert появился новый столбец True. В нем содержатся безусловные действия, которые выполняются всегда. В-третьих, в первом столбце, кроме входных параметров и возвращаемого значения, появился еще один тип переменных — локальные переменные. Строго говоря, каждая строка без имени является анонимной локальной переменной (это наглядно продемонстрировано в таблицах юнит-теста, который был рассмотрен ранее). Но в некоторых случаях удобно дать строке некоторое имя, чтобы потом можно было использовать ее значение в последующих операциях и функциях.Итак, двигаясь сверху вниз и размышляя слева направо, мы приходим к такой последовательности действий:
- На основании типа атаки присвоить локальной переменной
powerзначение 5 или 4. - На основании признака неожиданности атаки, присвоить анонимной локальной переменной значение 3 или 2.
- Присвоить локальной переменной
effectivenessрезультат произведения двух переменных, значения которых были определены в пунктах 1 и 2. - Если
attack == Magic, Вычесть изeffectivenessзначение переменнойdefense. - Если
attack == Magic & defense <= 0, вернуть значение 0. - Если
attack == Magic & defense >= 1, вернуть результат вычитанияeffectiveness - defense. - Если
attack == Melee, вернуть результат выраженияeffectiveness / defense * 2.
True (пункт 3) выполняется всегда, когда до нее доходит очередь — она не зависит от выполнения того или иного условия. Все остальные операции выбираются из столбца, условие которого является истинным для текущего набора входных параметров.Горизонтальные линии отображают потоки данных между условиями, определенными в таблице. Таким образом, наличие горизонтальной линии всегда свидетельствует об использовании данных, посчитанных в одном условии (или безусловно) в вычислениях с другим условием.
Визуальное сравнение исходного кода метода
damage и соответствующей ему схематической таблицы при одном и том же размере шрифта:
Слева сравнивается размер конструкции на экране при двух различных способах записи, а справа наглядно показано переплетение логики метода. Так как в текстовой записи логики программы присутствует только одно измерение, в нашем примере возникает «пробка» — зеленый участок посередине помещен между двумя условными блоками. Это немного затрудняет восприятие кода, если мы хотим, например, узнать результат выполнения при выполнении условия
attack == Magic. В случае схематической таблицы, логика и действия расположены на двух различных осях, ортогональных друг другу. И здесь мы приходим к фундаментальному принципу концепции схематических таблиц — представление кода в двух измерениях, вместо одного.
На горизонтальной оси таблицы осуществляется принятие решений. Для записи условий используется семантика булевой алгебры.
На вертикальной оси выполняются действия, которые записываются в виде графа функций, связанных между собой посредством входных параметров и возвращаемых значений.
Если вы все еще скептически относитесь к концепции схематических таблиц, предлагаю вам взглянуть на следующий рисунок.

Оказывается, что такие виды условных конструкций, как вложенные if-then-else условия, switch-выражения и даже полиморфизм (не рассмотренный здесь), — все они сводятся к единому виду при использовании схематических таблиц. На мой взгляд, это хороший знак. Здесь будет уместным привести высказывание Альберта Эйнштейна:
Все должно быть простым, насколько это возможно, но не проще.
В данной заметке я не рассматривал полиморфизм, так как он не вносит больших изменений в структуру таблицы. Пример того, как заменить перекрытие (overriding) метода на языке Java записью в виде схематической таблицы, начинается на видео презентации с 29-й минуты.
Заключение
Описанная концепция является одной из нескольких интересных возможностей, положенных в основу разрабатываемого Джонатаном языка программирования Coherence. Скриншоты в статье были сделаны с видео презентации. Автор разработал оболочку, которая предоставляет средства для интерактивной работы со схематическими таблицами, их редактирования и выполнения, а также написания юнит-тестов. Увидеть все это в действии можно на видео. Автор также выложил исходный код оболочки (написанный на С#) вместе с исполняемым файлом для ОС Windows. [скачать]
Дополнительные материалы по теме, включая статью с формальным описанием концепции схематических таблиц, можно найти на сайте www.subtextual.org. У автора также есть блог. Хоть он и редко обновляется, там можно найти описание и других интересных идей, таких как, например, co-actions.
Чтобы лучше понять идеологию Джонатана, можно ознакомиться с его довольно-таки радикальным манифестом, в котором он высказывает доводы против принятой в настоящее время записи логики программы в виде исходного кода и предлагает новые пути развития программирования.
Благодарю за внимание.
UPD:
В комментариях люди высказывают сомнения по поводу целесообразности применения схематических таблиц на практике. Попробую немного прояснить ситуацию.
Данный метод записи логики программы ни в коем случае не позиционируется как завершенная разработка, для которой осталось только написать IDE с компилятором и пустить ее в массы. На данный момент это только концепция. На мой взгляд, она наталкивает на некоторые размышления о текущем положении дел в области программирования. Я решил, что хабрасообществу будет интересно узнать о ней, так как в последнее время из новый веяний в области мы можем наблюдать лишь появление новых языков, которые основываются на уже существующих парадигмах программирования, не смотря на то, что включают в себя механизмы для более простой организации параллельных вычислений.
UPD2:
Прошу прощения за дезинформацию. Исходники оболочки, написанный на C#, и исполняемый файл для ОС Windows можно скачать с сайта проекта, см. первый вопрос в разделе FAQ. Subtext — это ее старое название, сейчас проект носит имя Coherence.
P. S. Если у вас есть замечания по стилю изложения или оформлению статьи, не стесняйтесь писать их в комментариях или мне лично. Я буду рад любой критике.
24.01.2010 03:17+0300
