Претендент на теорию всего — Е8 геометрия

Единая геометрическая теория — часть 1

Теории объединения взаимодействий

В самом деле вопрос о теории всего или теории объединения всех фундаментальных взаимодействий (электромагнитное, слабое, сильное, гравитационное, кстати первые три поддаются нынешним теориям объединения) в единую теорию является наверное одним из основных вопросов современной теоретической физики. В этой статье пойдет речь о кандидате на решение данного вопроса, а именно о единой геометрической теории E8. Что же это такое?
Но для начала проследим путь к великому объединению. Первой из теорий взаимодействий стала теория электромагнетизма, созданная Максвеллом. Затем Эйнштейн сформулировал общую теорию относительности, описывающую гравитационное поле. Появилась идея построения единой теории фундаментальных взаимодействий (которых на тот момент было известно только два), подобно тому как Максвеллу удалось создать общее описание электрических и магнитных явлений. Такая единая теория объединила бы гравитацию и электромагнетизм в качестве частных проявлений некоего единого взаимодействия.
С появлением квантовой механики задача усложнилась, так как общие эффекты этих двух теории объединить не удавалась в рамках одной теории.
Позже были выяснены природа как слабого, так и сильного взаимодействия. В 1967 году Саламом и Вайнбергом была создана теория электрослабого взаимодействия, объединившая электромагнетизм и слабые взаимодействия. Позднее в 1973 году была предложена теория сильного взаимодействия (квантовая хромодинамика). На их основе была построена Стандартная Модель элементарных частиц, описывающая электромагнитное, слабые и сильное взаимодействия. На данный момент Стандартная модель является общепринятой теорией для описания взаимодействий.

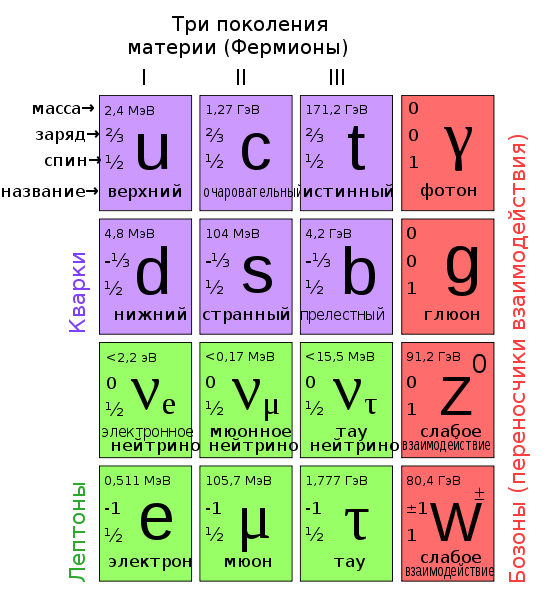
Встал вопрос: как соединить теорию гравитации и Стандартную модель. Этот вопрос остается открытым. Существует множество предположений по поводу решения этой проблемы. Теория струн, М-теория, петлевая квантовая гравитация, теория суперструн, а так же рассматривая нами сегодня теория E8.

Единый геометрический объект

Можно предположить, что на микроуровне все взаимодействия и их переносчики представляют собой некий сложный универсальный геометрический объект.
Чтобы продолжить разговор попробуем разобрать необходимые нам понятия геометрии фундаментальных взаимодействий.

Группы

Рассмотрим довольно простой пример, который иллюстрирует понятие группы и далее группы Ли. Группы Ли были созданы в теории алгебры Ли норвежским математиком Софиусом Ли. Стоит сказать, что норвежские математики внесли огромный вклад в развитие теории групп. Вернемся к примеру. Под наш разбор попадет простейшая геометрическая фигура — квадрат. Рассмотрим поворот квадрата на 90 градусов в плоскости самой фигуры. Поворачивать будем n-ое количество раз, отметим тут факт симметрии наших преобразований.

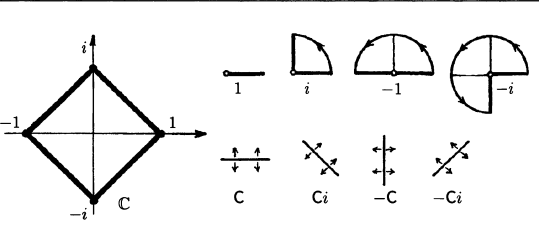
Повороты будем описывать с помощью комплексных чисел как на рисунке. И соответственно сопоставим вершинам комплексные числа 1, i, -1, -i, тогда повороту на 90 градусов будем сопоставлять умножение на i. Степени числа i и будут нашими поворотами. Всего можем получить четыре различных точки плоскости, имеем четыре элемента. Умножение любых двух из них будет давать результат, который так же является одним из этих четырех элементов. Именно эти четыре степени числа i могут послужить примером конечной группы. Группу определяет так же правило умножения элементовa a(bc)=(ab)c. Обязательно существование единичного элемента и обратного элемента. Если же мы добавим сюда свойство коммутативности умножения ab=ba, то такую группу называют абелевой группой(Абель кстати тоже норвежский математик). Наша группа очевидно абелева, так как комплексные числа обладают свойством коммутативности умножения.
Теперь введем операцию отражения, изменяющую ориентацию нашего квадрата, а именно поворот вокруг оси, которому алгебраически соответствует комплексное сопряжение — С. Будут очевидно справедливы следующие соотношения:
Ci=-iC, C(-1)=(-1)C, C(-i)=iC, CC=1 => i^4=1, C^2=1 Ci=i^3C
Из последнего можно заметить, что относительно операции комплексного сопряжения эта группа не абелева.
Если рассмотреть сферы и ее вращения, то получим бесконечное количество разных конфигураций, так как мы можем вращать ее на любой угол, получая все тот же объект симметричный исходному. Именно такая группа называется непрерывной или группой Ли.
Группа Ли очень важна для понимания геометрии фундаментальных взаимодействий.

Общие соображения и вводное слово

В 2007 г. физик Энтони Гаррет Лиси написал ставшую предметом широких дискуссий среди физиков–теоретиков статью.
Многие современные ученые полагают, что попытка объединить теорию относительности Эйнштейна и квантовую теорию должна радикально изменить наше понимание реальности. Однако в противовес им Лиси полагает, что геометрическое описание современной квантовой физики может быть расширено с включением в него и гравитационной теории, приведя к созданию долгожданной единой теории всех взаимодействий.
Почему геометрия? Вопрос имеет место быть. Попытаемся на него ответить. Для того чтобы объяснить суть теории E8, нам необходимо знание некоторых широко используемых геометрических принципов, которые управляют всеми известными частицами и взаимодействиями. Геометрия изучает формы. Однако применительно к задачам фундаментальной физики каждый из нас может спросить, формы чего. Платон представлял основные элементы – землю и воздух – как маленькие кубы и октаэдры (восьмигранники). Точно так же в современной физике геометрические объекты, сопоставленные с элементарными частицами, есть правильные фигуры, существующие как бы в некотором абстрактном воображаемом пространстве. Разумеется, мы не можем видеть эти фигуры – они принадлежат математическому пространству, – однако нам дано выявить обусловленные ими эффекты уже в нашем реальном мире. Прямая аналогия с геометрическим понятийным аппаратом позволяет оперировать трудоемкими вещами легче и быстрее.

Геометрия Стандартной модели

Основная геометрическая идея, лежащая в основе Стандартной модели, заключается в том, что каждой точке нашего пространства–времени сопоставляются некие формы, называемые слоями (fibers). Каждый слой соответствует своему типу частиц. Для наглядности нашу Вселенную можно представить в виде терракотовой фигурки, сплошь покрытой ростками. Вся ее поверхность – аналог нашего четырехмерного пространства–времени, а отростки – слои. Вся фигурка целиком – наше реальное пространство–время и слои–отростки – называется многомерным пространством расслоения (fiber bundle). Слои, очевидно, лежат вне нашего пространства; математически они представляют собой внешние пространства, «прикрепленные» к каждой точке нашего обычного пространства, и обладают различными формами в зависимости от свойств частиц.

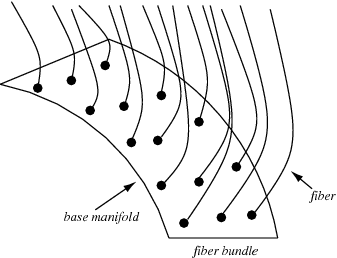
Эта наглядная геометрическая концепция, впервые предложенная в 1918 г. математиком Германом Вейлем, сегодня стала прочно устоявшимся физическим принципом. Слои внешнего пространства отличаются от предполагаемых пространственных измерений струнной теории, обладая фиксированной формой. Их динамика определяется способом прикрепления к нашему четырехмерному миру.

Электромагнитное взаимодействие

Рассмотрим с точки зрения геометрии электромагнитное взаимодействие. Электромагнитное поле присутствует везде, этот факт обусловлен тем, что форма слоев есть окружность.

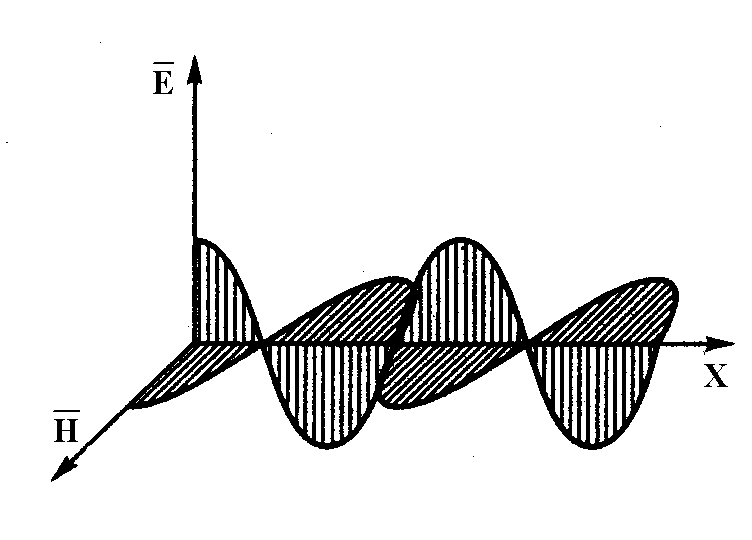
Спроецировав на одну ось действительно получим полуокружности. В рамках данного подхода получим некие окружности, которые обвивают луч.

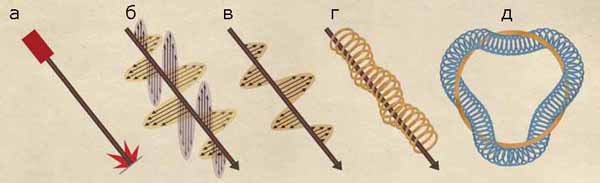
Они обладают симметрией, называемой U(1), и представляет собой простейший пример группы Ли. Окружность обладает единственной симметрией: при ее повороте вокруг своего центра она переходит сама в себя, не меняясь. Вращение окружности вокруг своего центра на малый угол называется генератором группы Ли. Следуя генератору как указанию стрелки компаса, можно осуществлять произвольные вращения вокруг центра.
Пространство расслоения для электромагнитных взаимодействий представляет собой окружности, «присоединенные» к каждой точке нашего реального пространства–времени. Важно отметить, что каждая окружность может вращаться на небольшие углы относительно своих пространственно–временных «соседей». Так называемое поле связности для пространства расслоения описывает, как соседние слои связаны с помощью своих симметричных поворотов. Поля электрического и магнитного взаимодействий заполняют пространство–время согласно кривизне своих слоев; другими словами, электрическое и магнитное поля следуют поворотам круговых слоев в пространстве–времени. Электромагнитная волна – это волнообразные колебания указанных окружностей в пространстве–времени. Один квант электромагнитной волны (фотон) – это распространяющаяся частица света.
Каждый сорт элементарных частиц соответствует разному слою в пространстве–времени. У упомянутой нами фигурки много разных типов отростков. Так, все на свете электроны происходят от поворота слоя одного вида – что, в частности, объясняет, почему все электроны одинаковые. Слои электрически заряженных частиц, таких как электрон, поворачиваются вокруг круговых слоев электромагнитных взаимодействий как нити вокруг винта. Скорость поворотов соответствующего частице слоя вокруг окружности эквивалентна электрическому заряду этой частицы, т.е. характеризует степень ее взаимодействия с электромагнитным полем.
Поскольку обороты вокруг окружности обладают периодичностью, заряды соответствующей частицы суть целые числа, умноженные на некую стандартную единицу электрического заряда. Среди элементарных частиц вещества, называемых фермионами, электроны обладают электрическим зарядом –1 (три полных оборота), верхние кварки обладают электрическим зарядом +2/3 (два противоположных поворота), нижние кварки – электрическим зарядом –1/3 (один поворот) и нейтрино – 0. Частицы антиматерии, такие как позитроны и антикварки, вращаются вокруг электромагнитной окружности в противоположную сторону, что дает этим частицам противоположный электрический заряд.
При столкновении частицы могут преобразовываться в частицы других типов, но их общий электромагнитный заряд до и после взаимодействия не изменяется. Это важное свойство можно интерпретировать как следствие геометрии слоев: когда любые две частицы встречаются, их повороты складываются. Таким образом, картина пространства расслоения хорошо объясняет то, что мы знаем об электромагнетизме. Электрические заряды описывают геометрическую структуру совокупного электромагнитного поля и пространства расслоения для вещества, определяя, какие взаимодействия возможны между электрически заряженными частицами.

На сегодня все. Напоследок несколько видео.



P.S. Во второй части рассмотрим гравитацию как геометрический объект. А так же увидим опровержение данной теории в научно-популярном контексте.

По материалам:
1. «В Мире Науки» №3 2011
2. Пенроуз Р. «Путь к реальности или законы, управляющие вселенной»