Ни о чём →
Быстрое сравнение гистограмм
Во многих задачах распознавания образов, моделирования требуется быстро сравнивать гистограммы, ряды или многомерные векторы. Причем, сравнение нужно не строгое а с определенной степенью похожести. В статье предлагается компактный метод хранения и быстрого поиска близких векторов, гистограмм, рядов.
Пусть дан ряд чисел X=(X1,X2,X3,X4, ..,Xn). Будем называть его гистограммой (хотя это может быть произвольный упорядоченный набор значений, вектор). На комопненты гистограммы наложим ограничение — все значения лежат в фиксированном, конечном интервале. В наших примерах это будет интервал от 0 до 100.
Итак, имеется большой набор гистограмм и есть шаблонная гистограмма, к которой мы хотим найти наиболее похожую гистограмму из имеющегося набора.
Введем меру различий двух гистограмм, равной максимальной разнице между двумя соответствующими компонентами (эта мера называется также расстоянием Чебышева):
d(X, Y) = max(|Xi-Yi|)
При решении задачи поиска «в лоб» мы будем перебирать гистограммы из заданного набора, и сравнивать их с шаблоном. Для каждого сравнения мы будем перебирать компоненты гистограмм, считать их разности и находить максимальную из них. Понятно, что это долго, а нам бы хотелось ускорить этот процесс.
Для быстрого сравнения гистограмм, оптимально было бы закодировать гистограмму в виде одного числа. С числами процессор справляется быстрее, чем с массивами, и поиск существенно ускорился бы.
Пусть максимальное допустимое значение расстояния между гистограммами MaxD – задано заранее. Мы бы могли квантовать каждый компонент гистограммы до величин, сравнимых с MaxD, и закодировать их битами числа. По одному или нескольким бит на значение. Тогда результирующее число будет содержать огрубленные значения гистограммы. А точности огрубления должно хватить для поиска гистограмм, с заданным максимальным расстоянием. Пусть, например, MaxD=33, тогда значения компоненты, меньшие 33 можно закодировать двумя битами 00, от 33 до 66 закодировать битами 01, от 66 до 100 – закодировать битами 10. При разрядности числа 64 бита мы бы могли хранить в нем 32 столбиков гистограммы, что в общем-то неплохо.

Теперь, если мы закодируем две гистограммы числами A и B, то близкие гистограммы дадут одинаковые числа, и мы сможем выяснить этот факт, просто сравнив A и B. Если разница между ними – нуль, то значит, исходные гистограммы были близки с точностью до MaxD.
Однако у такого метода есть очень большой недостаток. Да, если гистограммы далеки друг от друга, то A-B гарантированно не будет равно нулю. Но обратное утверждение не верно. Если разность не равна нулю, это еще не значит, что гистограммы далеки друг от друга. Если компонента близка к величине 33, то она равновероятно может попасть как в первый диапазон(00), так и в другой(01). В результате – почти одинаковые гистограммы будут иметь разные коды.
Итак, нам бы хотелось закодировать гистограмму так, что бы сравнение кодов гарантированно нам давало уверенность о близости или дальности гистограмм. Оказывается, такое представление существует. Оно аналогично предыдущему, но биты, кодирующие диапазоны – другие.
Пусть значения, попадающие в первый диапазон, кодируются битами 01, во второй – 00, в третий – 10:
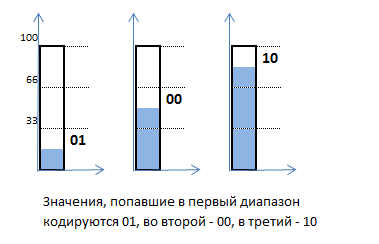
Тогда закодированная шаблонная гистограмма может иметь такой вид:
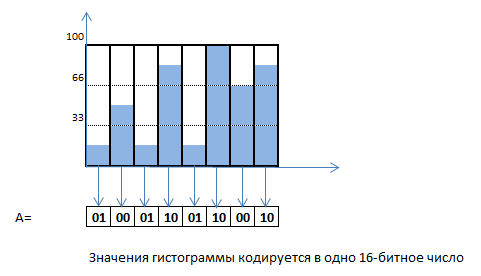
А вот гистограмма B, с которой мы будем сравнивать, будет кодироваться по-другому: значения до 33 – битами 10, от 33 до 66 – битами 00, от 66 до 100 – битами 01.

На первый взгляд кажется, что несимметричное кодирование неудобно, но на практике это проблем не вызовет, поскольку первый тип кодировки будет иметь только шаблонная гистограмма, а второй тип – все гистограммы хранящиеся в базе данных. Иной ситуации не потребуется.
Посмотрим, как ведет себя побитное пересечение введенных нами кодов:
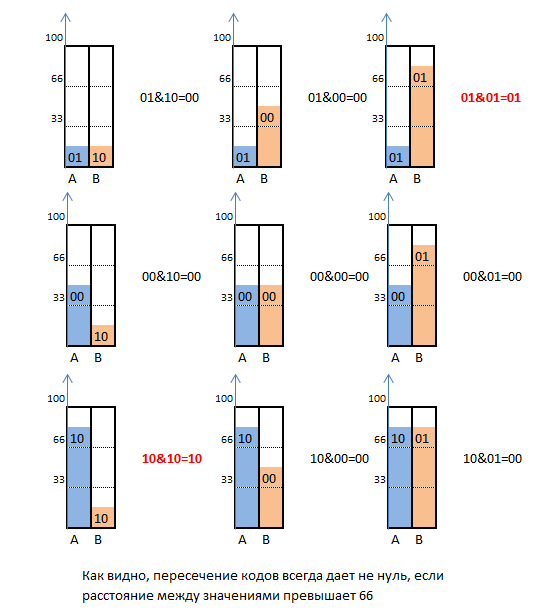
Оказывается, при таком способе кодирования, пересечение A&B гарантированно дает не нуль, если расстояние между компонентами более 66. Такое расстояние возможно, если один столбик – очень высокий и имеет код 10, а второй – очень низкий и тоже имеет код 10. А их пересечение 10&10=10 дает не нуль. Обратная ситуация – один столбик очень низкий (01), а другой – очень высокий (тоже 01). В этом случае объединение их кодов – тоже не нулевое: 01&01=01.
В остальных случаях пересечение будет давать нуль. Таком образом, нулевое значение A&B гарантирует, что расстояние между величинами не превышает 66.

Обратим внимание на то, что ненулевое значение может появиться не только в случае расстояния большего 66. К примеру, если один столбик имеет значение 32, а другой — 67, то A&B даст не нуль, хотя разница между ними 35. Таким образом, ненулевое значение A&B гарантирует что, что расстояние между гистограммами не менее 33.
Резюмируя, описанный способ кодирования обладает следующими свойствами:
1) A&B=0 -> d(X, Y)<66
2) A&B!=0 -> d(X, Y)>33
3) d(X, Y)>66 -> A&B!=0
4) d(X, Y)<33 -> A&B=0
Как видим, метод сравнения дает определенные гарантии относительно истинного расстояния между гистограммами. При этом, исключены такие ситуации, что близкие гистограммы (при расстоянии менее 33) будут классифицированы как далекие. С другой стороны, далекие гистограммы (расстояние более 66) — однозначно будут расценены как далекие. Гистограммы с расстоянием от 33 до 66 — могут попасть как в класс близких, так и в класс далеких.
С описанным способом хранения, поиск близких к шаблону гистограмм становится простым и очень быстрым. Если мы хотим отобрать все гистограммы, ближе чем 33 к нашему образцу, просто проверяем что A&B=0:
Для сравнения, тот же поиск «в лоб», выглядит примерно так:
Первый способ поиска дает прирост производительности примерно на порядок, по сравнению с «лобовым» подходом.
Оценим каков процент кандидатов на сравнение нам удастся отбросить.
Вероятность нулевой комбинации A&B для одной компоненты равна 7/9=0.777.
Для 16-ти компонентной гистограммы, вероятность нулевого A&B равна (7/9)^16 = 0.018. Это значит, что алгоритм отбирает около 2% из всех кандидатов для 16-ти компонентной гистограммы (разумеется, эта оценка исходит из предположения, что компоненты имеют случайное равномерное распределение, что в реальности, не совсем так).
Для 32-компонентной гистограммы будет отобран лишь один из 3000 кандидатов.
А что же с декартовым расстоянием? Оказывается и для него может оказатся полезным рассмотренный метод. Пользуясь нехитрыми преобразованиями, найдем связь между декартовым (обозначим его как r) и чебышевским расстояниями:
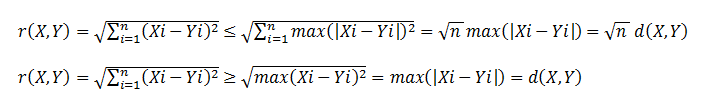
То есть
d(X,Y) <= r(X, Y) <=
Пусть дан ряд чисел X=(X1,X2,X3,X4, ..,Xn). Будем называть его гистограммой (хотя это может быть произвольный упорядоченный набор значений, вектор). На комопненты гистограммы наложим ограничение — все значения лежат в фиксированном, конечном интервале. В наших примерах это будет интервал от 0 до 100.
Итак, имеется большой набор гистограмм и есть шаблонная гистограмма, к которой мы хотим найти наиболее похожую гистограмму из имеющегося набора.
Введем меру различий двух гистограмм, равной максимальной разнице между двумя соответствующими компонентами (эта мера называется также расстоянием Чебышева):
d(X, Y) = max(|Xi-Yi|)
При решении задачи поиска «в лоб» мы будем перебирать гистограммы из заданного набора, и сравнивать их с шаблоном. Для каждого сравнения мы будем перебирать компоненты гистограмм, считать их разности и находить максимальную из них. Понятно, что это долго, а нам бы хотелось ускорить этот процесс.
Идея первая
Для быстрого сравнения гистограмм, оптимально было бы закодировать гистограмму в виде одного числа. С числами процессор справляется быстрее, чем с массивами, и поиск существенно ускорился бы.
Пусть максимальное допустимое значение расстояния между гистограммами MaxD – задано заранее. Мы бы могли квантовать каждый компонент гистограммы до величин, сравнимых с MaxD, и закодировать их битами числа. По одному или нескольким бит на значение. Тогда результирующее число будет содержать огрубленные значения гистограммы. А точности огрубления должно хватить для поиска гистограмм, с заданным максимальным расстоянием. Пусть, например, MaxD=33, тогда значения компоненты, меньшие 33 можно закодировать двумя битами 00, от 33 до 66 закодировать битами 01, от 66 до 100 – закодировать битами 10. При разрядности числа 64 бита мы бы могли хранить в нем 32 столбиков гистограммы, что в общем-то неплохо.

Теперь, если мы закодируем две гистограммы числами A и B, то близкие гистограммы дадут одинаковые числа, и мы сможем выяснить этот факт, просто сравнив A и B. Если разница между ними – нуль, то значит, исходные гистограммы были близки с точностью до MaxD.
Однако у такого метода есть очень большой недостаток. Да, если гистограммы далеки друг от друга, то A-B гарантированно не будет равно нулю. Но обратное утверждение не верно. Если разность не равна нулю, это еще не значит, что гистограммы далеки друг от друга. Если компонента близка к величине 33, то она равновероятно может попасть как в первый диапазон(00), так и в другой(01). В результате – почти одинаковые гистограммы будут иметь разные коды.
Идея вторая
Итак, нам бы хотелось закодировать гистограмму так, что бы сравнение кодов гарантированно нам давало уверенность о близости или дальности гистограмм. Оказывается, такое представление существует. Оно аналогично предыдущему, но биты, кодирующие диапазоны – другие.
Пусть значения, попадающие в первый диапазон, кодируются битами 01, во второй – 00, в третий – 10:

Тогда закодированная шаблонная гистограмма может иметь такой вид:

А вот гистограмма B, с которой мы будем сравнивать, будет кодироваться по-другому: значения до 33 – битами 10, от 33 до 66 – битами 00, от 66 до 100 – битами 01.

На первый взгляд кажется, что несимметричное кодирование неудобно, но на практике это проблем не вызовет, поскольку первый тип кодировки будет иметь только шаблонная гистограмма, а второй тип – все гистограммы хранящиеся в базе данных. Иной ситуации не потребуется.
Посмотрим, как ведет себя побитное пересечение введенных нами кодов:

Оказывается, при таком способе кодирования, пересечение A&B гарантированно дает не нуль, если расстояние между компонентами более 66. Такое расстояние возможно, если один столбик – очень высокий и имеет код 10, а второй – очень низкий и тоже имеет код 10. А их пересечение 10&10=10 дает не нуль. Обратная ситуация – один столбик очень низкий (01), а другой – очень высокий (тоже 01). В этом случае объединение их кодов – тоже не нулевое: 01&01=01.
В остальных случаях пересечение будет давать нуль. Таком образом, нулевое значение A&B гарантирует, что расстояние между величинами не превышает 66.

Обратим внимание на то, что ненулевое значение может появиться не только в случае расстояния большего 66. К примеру, если один столбик имеет значение 32, а другой — 67, то A&B даст не нуль, хотя разница между ними 35. Таким образом, ненулевое значение A&B гарантирует что, что расстояние между гистограммами не менее 33.
Резюмируя, описанный способ кодирования обладает следующими свойствами:
1) A&B=0 -> d(X, Y)<66
2) A&B!=0 -> d(X, Y)>33
3) d(X, Y)>66 -> A&B!=0
4) d(X, Y)<33 -> A&B=0
Как видим, метод сравнения дает определенные гарантии относительно истинного расстояния между гистограммами. При этом, исключены такие ситуации, что близкие гистограммы (при расстоянии менее 33) будут классифицированы как далекие. С другой стороны, далекие гистограммы (расстояние более 66) — однозначно будут расценены как далекие. Гистограммы с расстоянием от 33 до 66 — могут попасть как в класс близких, так и в класс далеких.
Поиск и сравнение
С описанным способом хранения, поиск близких к шаблону гистограмм становится простым и очень быстрым. Если мы хотим отобрать все гистограммы, ближе чем 33 к нашему образцу, просто проверяем что A&B=0:
for (int i = 0; i < samples.Count; i++)
{
if( template.a & samples[i].b == 0)
...//гистограммы близки (сюда попадают ВСЕ гистограммы ближе 33, и часть гистограмм с расстоянием до 66)
}Для сравнения, тот же поиск «в лоб», выглядит примерно так:
for (int i = 0; i < samples.Count; i++)
{
bool key= false;
for (int j = 0; j < 16; j++)
if (Math.Abs(template.bytes[j] - samples[i].bytes[j])>170)
{
key = true;
break;
}
if(!key)
....//гистограммы близки
}Первый способ поиска дает прирост производительности примерно на порядок, по сравнению с «лобовым» подходом.
Оценим каков процент кандидатов на сравнение нам удастся отбросить.
Вероятность нулевой комбинации A&B для одной компоненты равна 7/9=0.777.
Для 16-ти компонентной гистограммы, вероятность нулевого A&B равна (7/9)^16 = 0.018. Это значит, что алгоритм отбирает около 2% из всех кандидатов для 16-ти компонентной гистограммы (разумеется, эта оценка исходит из предположения, что компоненты имеют случайное равномерное распределение, что в реальности, не совсем так).
Для 32-компонентной гистограммы будет отобран лишь один из 3000 кандидатов.
Применение метода для декартового расстояния
А что же с декартовым расстоянием? Оказывается и для него может оказатся полезным рассмотренный метод. Пользуясь нехитрыми преобразованиями, найдем связь между декартовым (обозначим его как r) и чебышевским расстояниями:
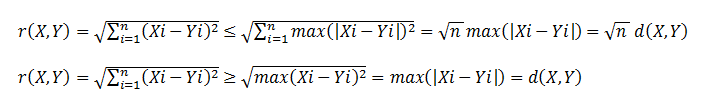
То есть
d(X,Y) <= r(X, Y) <=
24.12.2009 15:08+0300
